علم ریاضی
این وبلاگ جهت استفاده علاقمندان به ریاضی ایجاد شده است.علم ریاضی
این وبلاگ جهت استفاده علاقمندان به ریاضی ایجاد شده است.manifold
A manifold is a topological space that is locally Euclidean (i.e., around every point, there is a neighborhood that is topologically the same as the open unit ball in ). To illustrate this idea, consider the ancient belief that the Earth was flat as contrasted with the modern evidence that it is round. The discrepancy arises essentially from the fact that on the small scales that we see, the Earth does indeed look flat. In general, any object that is nearly "flat" on small scales is a manifold, and so manifolds constitute a generalization of objects we could live on in which we would encounter the round/flat Earth problem, as first codified by Poincaré.A manifold is a topological space that is locally Euclidean (i.e., around every point, there is a neighborhood that is topologically the same as the open unit ball in ). To illustrate this idea, consider the ancient belief that the Earth was flat as contrasted with the modern evidence that it is round. The discrepancy arises essentially from the fact that on the small scales that we see, the Earth does indeed look flat. In general, any object that is nearly "flat" on small scales is a manifold, and so manifolds constitute a generalization of objects we could live on in which we would encounter the round/flat Earth problem, as first codified by Poincaré.
More concisely, any object that can be "charted" is a manifold.
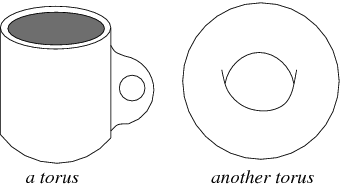
One of the goals of topology is to find ways of distinguishing manifolds. For instance, a circle is topologically the same as any closed loop, no matter how different these two manifolds may appear. Similarly, the surface of a coffee mug with a handle is topologically the same as the surface of the donut, and this type of surface is called a (one-handled) torus.
As a topological space, a manifold can be compact or noncompact, and connected or disconnected. Commonly, the unqualified term "manifold"is used to mean "manifold with boundary." This is the usage followed in this work. However, an author will sometimes be more precise and use the term open manifold for a noncompact manifold without boundary or closed manifold for a compact manifold with boundary.
If a manifold contains its own boundary, it is called, not surprisingly, a "manifold with boundary." The closed unit ball in is a manifold with boundary, and its boundary is the unit sphere. The concept can be generalized to manifolds with corners. By definition, every point on a manifold has a neighborhood together with a homeomorphism of that neighborhood with an open ball in . In addition, a manifold must have a second countable topology. Unless otherwise indicated, a manifold is assumed to have finite dimension , for a positive integer.
Smooth manifolds (also called differentiable manifolds) are manifolds for which overlapping charts "relate smoothly" to each other, meaning that the inverse of one followed by the other is an infinitely differentiable map from Euclidean space to itself. Manifolds arise naturally in a variety of mathematical and physical applications as "global objects." For example, in order to precisely describe all the configurations of a robot arm or all the possible positions and momenta of a rocket, an object is needed to store all of these parameters. The objects that crop up are manifolds. From the geometric perspective, manifolds represent the profound idea having to do with global versus local properties.
The basic example of a manifold is Euclidean space, and many of its properties carry over to manifolds. In addition, any smooth boundary of a subset of Euclidean space, like the circle or the sphere, is a manifold. Manifolds are therefore of interest in the study of geometry, topology, and analysis.
A submanifold is a subset of a manifold that is itself a manifold, but has smaller dimension. For example, the equator of a sphere is a submanifold. Many common examples of manifolds are submanifolds of Euclidean space. In fact, Whitney showed in the 1930s that any manifold can be embedded in , where .
A manifold may be endowed with more structure than a locally Euclidean topology. For example, it could be smooth, complex, or even algebraic (in order of specificity). A smooth manifold with a metric is called a Riemannian manifold, and one with a symplectic structure is called a symplectic manifold. Finally, a complex manifold with a Kähler structure is called a Kähler manifold.