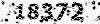اعداد روندا(Rhonda)

تعریف:عدد طبیعی n یک عدد روندا در مبنای B (عدد طبیعی) نامیده می‌شود اگر حاصل‌ضرب ارقام n در مبنای Bمساوی B برابر مجموع عوامل اول n باشد.نتیجه ی فوری از تعریف این است که اگر n در مبنای B روندا باشد،تمامی ارقام n در مبنای B غیر صفرند.

مثال: 25662 یک عدد روندا در مبنای 10 است،نمایش آن به صورت حاصل ضرب عوامل اول چنین است:

47 × 13 × 7 × 3 × 2 = 25662

و هم چنین داریم:

(47+13+7+3+2)×10 = 2×6×6×5×2.

و هم چنین داریم:

(47+13+7+3+2)×10 = 2×6×6×5×2.

چند عدد روندای دیگر در مبنای 10 عبارت هستند از:

5824 و 5664 و 5439 و 5265 و 4752 و 2835 و 1568

نکته:برای مبناهایی که عدد اول هستند،عدد روندایی وجود ندارد،چرا که برای عدد اول دلخواه p،p هیچ حاصل ضربی از اعداد طبیعی کوچک تر از خود را عاد نمی کند.

در جدول زیر چند عدد روندا در مبناهای ذکر شده را آورده ایم:

عدد 560 کوچک ترین عدد روندا است که در مبنای 12 روندا می‌باشد(توجه کنید که ارقام 560 در مبنای 12 عبارت هستند از:8و10و3)؛اعدادی طبیعی وجود دارند که برای بیش از یک مبنا،روندا هستند. مثلاً عدد 1000 کوچک ترین این اعداد است که برای مبناهای 16 و 36 روندا است.

تعریف:برای عدد طبیعی n،نمایش‌ دهنده‌ی مجموع عوامل اول n می‌باشد.
قضیه:تعداد نامتناهی عدد روندا وجود دارد.
اثبات:برای هر عدد طبیعی 5<m، یک عدد روندا در مبنای می باشد که در آن،عدد طبیعی k ریشه ی معادله ی زیر است:

توجه کنید که چون برای هر n، (چرا؟)پس برای هر 5<m،طرف راست معادله ی فوق مثبت بوده(مجموع سه جمله ی شامل Sopf در طرف راست معادله ،حداکثر برابر 3+6m بوده که با تعیین علامت،برای هر 5<m،طرف راست معادله ی فوق مثبت خواهد بود.)و در نتیجه،معادله ی فوق همواره ریشه دارد.

مثال:

اگر در روابط فوق، 6=m قرار دهیم آن گاه از:

4= 13×2-7-5-7×6 =

داریم: 4=k و لذا یک عــدد رونــدا در مبنای می‌باشد.

نمایش N در مبنای B به صورت زیر است:

حاصل ضرب ارقام N در مبنای B برابر است با:.(1)
از طرفی با توجه به تعریف N:

بنابراین B برابر مجموع عوامل اول N مساوی است با و با توجه به (1) مساوی با حاصل ضرب ارقام N در مبنای B می‌باشد.و این یعنی N یک عدد روندا در مبنای B است.

این بحث نشان می دهد که اعداد روندا نامتناهی هستند.

منابع:
www.mathworld.wolfram.com

www.mathpages.com