مثالی برای استقرای تعمیم یافته

مثال: نشان دهید در هر n ضلعی محدب تعداد قطرها برابر است با: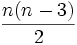

پاسخ: می دانیم یک 3 ضلعی محدب، مثلث دارای هیچ قطری نمی باشد و چهار ضلعی محدب دارای
دو قطر است. به این ترتیب حکم را برای n>3 اثبات می کنیم. مرحله اول (مبنا) را با n=4 آغاز می کنیم:
1-
حال فرض می کنیم که حکم برای n=k درست باشد، یعنی تعداد قطرهای هر k ضلعی محدب برابر باشد با:

نشان می دهیم که حکم برای n=k+1 هم درست است، یعنی تعداد قطرهای هر k+1 ضلعی محدب برابر است با:

برای اثبات سعی می کنی به گونه ای از فرض استقرا استفاده کنیم. به این صورت که می دانیم که اگر به تعداد ضلعهای یک n ضلعی، یک ضلع اضافه کنیم یا به تعداد رئوس آن یک راس اضافه کنیم به تعداد قطرهای آن n-1 واحد اضافه می شود. لذا:

(k-1)+تعداد قطرهای k ضلعی محدب=تعداد قطرهای k+1 ضلعی محدب

بنابراین رابطه زیر برقرار است:

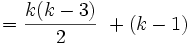تعداد قطرهای k+1 ضلعی محدب

و لذا حکم برای هر n>3 برقرار است.