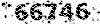اصل استقرای قوی ریاضی:
اصل استقرای قوی ریاضی:
صورتی دیگر از اصل استقرای ریاضی به شکل زیر مطرح می شود، که به اصل استقرای قوی ریاضی موسوم است. این اصل با اصل استقرای ریاضی و در نتیجه با اصل خوش ترتیبی معادل است.
اگر S زیرمجموعه ای از اعداد طبیعی باشد، به طوری که:
1- عدد یک عضوی از مجموعه S باشد.
2- اگر اعداد طبیعی کوچکتر از n در مجموعه S باشند، آنگاه n نیز عضو S باشد
در این صورت هر عدد طبیعی عضوی از S است و به عبارت دیگر S همان مجموعه اعداد طبیعی است.
- لازم به تذکر است در ریاضیات برای اثبات احکام طبیعی بیشتر از اصل استقرای قوی ریاضی استفاده میشود.
روش اثبات احکام بوسیله اصل استقرای قوی ریاضی:
1- درستی حکم را برای n=1 بررسی می کنیم.
2- نشان می دهیم که اگر حکم داده شده به ازا هر عدد طبیعی k که (k<n) برقرار باشد، نگاه برای n نیز درست است.
با یک مثال روش اثبات را بررسی می کنیم:
دنباله 
به دنباله لوکا معروف است که در بین جملات آن رابطه بازگشتی زیر برقرار است:
با استفاده از اصل استقرای قوی ریاضی نشان می دهیم که برای هر عدد طبیعی n را بطه زیر برقرار است:
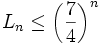
پاسخ: اگر
آنگاه 1و2 عضوی از S می باشند زیرا نامساویهای:
درست می باشند.(مرحله مبنا)
حال فرض میکنیم (فرض استقرا)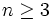 
و به ازای هر عدد طبیعی k که k، k<n در مجموعه S قرار دارد. بنابراین:
لذا چون 
پس:
و از طرفی دیگر:
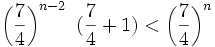
و لــذا:
یعنی n نیز در مجموعه S قرار دارد، پس مجموعه S همان مجموعه اعداد طبیعی است. و لذا برای هر عدد طبیعی n حکم برقرار است.
- لازم به توضیح است که از این اصل هم می توان برای اثبات برخی قضایای هندسه استفاده کرد و در ضمن می توان احکامی طبیعی که از یک هم آغاز نمی شوند را به این وسیله اثبات نمود.
(8 لایک)
