معادله هذلولی

معادله ی هذلولی

با در نظر گرفتن دو نقطه ی ثابت 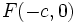و موسوم به کانون ها و مقدار ثابت 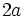، آن گاه نقطه ای چون بر هذلولی واقع است اگر و تنها اگر:

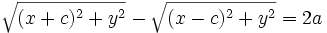
یا

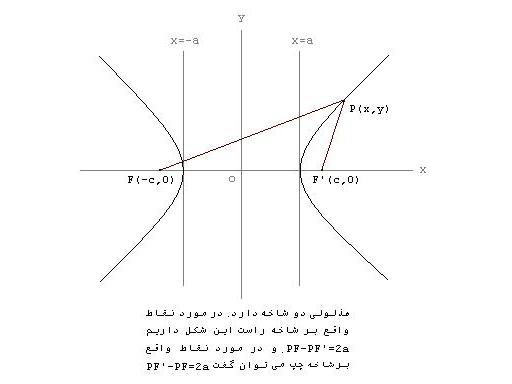
معادله ی دوم نظیر معادله ی اول می باشد، با این تفاوت که به جای 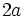، 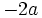قرار گرفته است. لذا می توان در اولی نوشت ، پس:

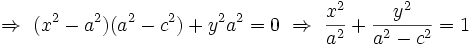
در این جا 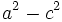منفی است زیرا تفاضل دو ضلع مثلث 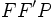از ضلع سوم کوچکتر است یعنی . لذا 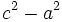مثبت است و یک ریشه ی دوم حقیقی مثبت دارد که آن را با 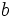نمایش می دهند، پس: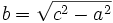
بنابر این معادله ی هذلولی به صورت زیر خواهد بود:

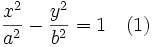
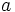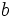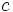که شبیه معادله ی بیضی است. اختلاف آن ها تنها در علامت منفی موجود در معادله ی هذلولی و رابطه ی جدید بین ، و است.

نکته 1: هذلولی نسبت به هر دو محور و نسبت به مبدا متقارن است و با محور 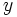تقاطعی ندارد. در واقع هیچ بخشی از خم بین خطوط 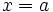و 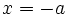قرار نمی گیرد.

نکته 2: فاصله های 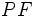و 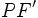از روابط زیر به دست می آیند:

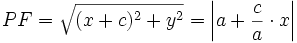
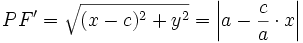
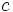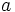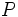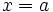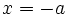در این جا از بزرگتر است و یا در سمت راست خط قرار می گیرد (یعنی)، یا در سمت چپ خط ( یعنی).

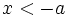نکته 3 : وقتی 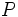در سمت راست خط 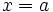قرار داشته باشد رابطه ی 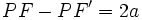و اگر در سمت چپ 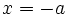واقع باشد رابطه ی 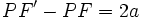برقرار است.

---

مجانب ها

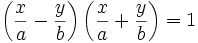
یا

نوشت.

الف) تحلیل معادله ی 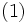نشان می دهد که یکی از شاخه های خم در ربع اول قرار داشته و تا بی نهایت امتداد دارد. اگر نقطه ی 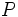واقع بر این شاخه رفته رفته از مبدا دور شود، و 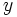بی نهایت می شوند و عبارت سمت راست معادله ی 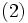به صفر نزدیک می شود. پس طرف چپ هم باید همین وضع را پیدا کند. در نتیجه:

ب) وقتی 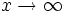، مشاهده می شود که:

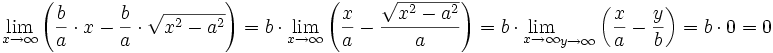
چون فاصله ی قائم بین خط و هذلولی وقتی 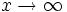، به صفر میل می کند، فاصله ی عمودی بین نقاط هذلولی و خط 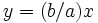نیز به صفر میل می کند. بنابراین از بندهای (الف) و (ب) نتیجه می شود که خط 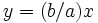مجانب هذلولی است.
بنابر تقارن، خط 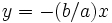نیز مجانب این هذلولی است.

نکته: گاه مجانب را چنان تعریف می کنند که لازم است وقتی 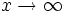، شیب خم به شیب مجانب نزدیک می شود. این تعریف نیز در این جا صادق است چرا که:

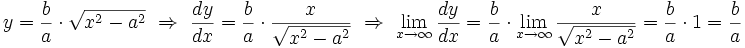
و این همان شیب مجانب 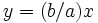است.

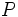تعریف: اگر هم زمان با دور شدن نقطه ای چون ( واقع بر یک خم ) از مبدا مختصات، فاصله ی آن با خط ثابتی به سمت صفر میل کند، آن گاه چنین خطی را مجانب خم نامند.

هذلولی 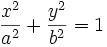دو مجانب دارد که عبارت اند از خط های .
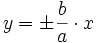چرا که عبارت سمت چپ معادله ی هذلولی را می توان تجزیه کرد و معادله را به صورت: