علم ریاضی
این وبلاگ جهت استفاده علاقمندان به ریاضی ایجاد شده است.علم ریاضی
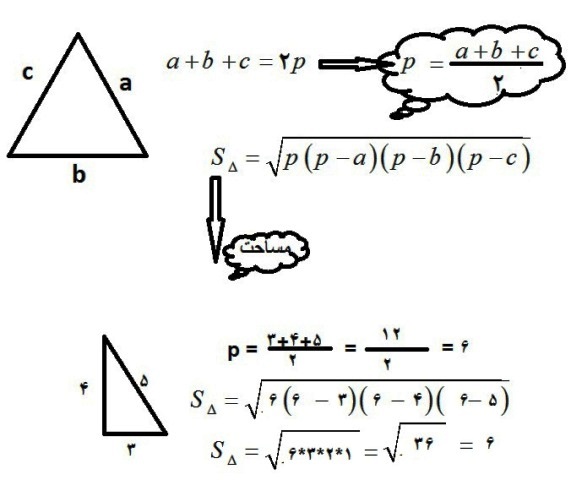
این وبلاگ جهت استفاده علاقمندان به ریاضی ایجاد شده است.بدست آوردن مساحت هر مثلث با دانستن مقدار هر 3 ضلع
می دانیم که مساحت مثلث در حالت کلی برابر 2/ (ارتفاع*قاعده)
در این روش ، فرمولی ارائه می شود که شما را قادر می سازد مساحت هر نوع مثلثی را با دانستن مقدار 3 ضلع آن محاسبه کنید .
فرض کنیم a و b و c اضلاع مثلث باشند و داشته باشیم :
اصطلاحات ریاضی به زبان تورکی
خوبه که همه ی این اصطلاحات رو به عنوان کسی که در آذربایجان زندگی می کنه هممون یاد بگیریم .
ریاضیات ............................ سای بیل .............................. say bil
بیضی ............................... یاستیْق اوُشاق ............... yastıquşaq
دایره ................................. یوُوارلاق ............................ yuvarlaq
مثلث ......................... اوچ گِن- اوچ بوُجاق ......... üçgen - üçbucaq
مربع ............................... دؤرد گِن ............................... dördgen
مستطیل ...................... جوت قوْل دؤرد گِن ......... cütqoldördgen
شش ضلعی ................... آلتیْ بوُجاقلیْ .................... altıbucaqlı
زاویه ................................ آچیْ .......................................... açı
صفر ................................ صیْفیْر ....................................... sıfır
عرض .............................. اِن ............................................. en
طول ............................... بوْی .......................................... boy
عدد- شماره- رقم ............ سای ........................................ say
قائم الزاویه ...................... دوز بوُجاق ......................... düzbucaq
گوشه – زاویه ................. بوُجاق .................................... bucaq
پایه – مخرج ...................... پایدا ...................................... payda
درصد ............................ . یوزدَه ...................................... yüzdə
افقی .............................. یاتای ....................................... yatay
عمودی ......................... دیک ........................................... dik
جمع+ ............................. آرتیْ .......................................... artı
منها- .............................. چیْخیْ ........................................ çıxı
ضرب× ........................... چارپیْ ...................................... çarpı
تقسیم÷ .......................... بؤلو ......................................... bölü
مساوی= ........................ اِئشیت ....................................... eşit
برگرفته شده از وبلاگ : http://riaziatrahnamai.blogfa.com
مقاله ای از پرویز شهریاری در مورد ریاضی
نخستین سفارش من این است که تا جایی که ممکن است، از کار انفرادی پرهیز کنیم و دانشاندوزی را به صورت یک کارگروهی درآوریم. باز هم از یک تجربه خود یاد کنم. این پیشآمد مربوط به زمانی است که من دانشجو بودم و درضمن در یکی از دبیرستانها تدریس میکردم. در آن دبیرستان، سه کلاس دوم دبیرستان وجود داشت که درس هندسه یکی از آنها به عهده من گذاشته شده بود. من، بعد از نزدیک به یک ماه، که با کلاس به اندازه کافی آشنا شده بودم، دانشآموزان را به گروههای سه نفری تقسیم کردم و در هر گروه یک دانشآموز به اصطلاح (قوی)، یک دانشآموز (متوسط) و یک دانشآموز (ضعیف) قرار دادم. رو به کلاس گفتم: من به فرد نمره نمیدهم و فرد را نمیشناسم. برای من گروه مطرح است. برای نمونه، وقتی شما امتحان بدهید، هرکسی باید برگ خودش را بنویسد، ولی من سه برگ هر گروه را به هم سنجاق میکنم، مجموع نمرههای سه گروه را به سه تقسیم میکنم و نتیجه را برای هر سه نفر میگذارم... حدس میزنید بازتاب این حرف در کلاس چگونه بود؟ دانشآموزان ضعیف خوشحال بودند، ولی فریاد دانشآموزان قوی بلند شد که: اگر دوست من درس نمیخواند، من چه گناهی کردهام؟ ولی من بیاحساس و بیتفاوت، روی تصمیم خود پای فشردم. دانشآموزان باور نکردند، ولی وقتی در سه ماه نخست، به همین ترتیب عمل کردم، به خود آمدند. البته حدس میزنید که من از طرف پدر و مادرها و مسئولان مدرسه، زیر چه فشار روحی قرار گرفتم. همه را تحمل کردم و در تصمیم خود تغییری ندادم. دانشآموزان به جان هم افتادند، وقتهای زیادی را در مدرسه میماندند و به هم کمک میکردند، به خانههای هم میرفتند، هر گروه از گروههای دیگر کمک میگرفت و در همه این موردها، دانشآموزان قوی به علت از دست دادن نمره خوب پیشقدم بودند. امتحان سه ماهه دوم را هم به همین ترتیب انجام دادم. تلاش دانشآموزان بیشتر شد و همراه با آن، فشار به من هم روزافزونتر بود، حتی در اثر شکایت پدر و مادرها، از طرف وزارت فرهنگ آن زمان، کسانی برای رسیدگی به این رفتار ظالمانه من به دبیرستان آمدند، ولی خوشبختانه تا بازرسها منتظر گزارشهای خود بودند، سال تحصیلی به پایان خود رسید و برنامه امتحانی آخر سال را دادند. نمرههای آخر سال را به ترتیب معمول دادم، یعنی نمره هرکسی را به خودش، نتیجه کار شگفتیآور بود. در کلاس من هیچکس نمره کمتر از 15 نداشت. همه از درس هندسه قبول شدند. و این معجزه کار گروهی بود. این تجربه نتیجه دیگری هم داشت. معلوم شد تقسیم دانشآموزان به (با استعداد) و (کم استعداد) آنطور که گمان میشود، ساده نیست و اگر روش کار درست باشد، بسیاری از (کماستعدادها) به گروه (بااستعدادها) میپیوندند، به جز همه این کارها، کارگروهی، رابطه انسانی بین دانشآموزان را تقویت میکند، از رقابتهای ناسالم آنها میکاهد و محیطی به وجود میآورد که هرکسی، خودش را مسئول سرنوشت دیگری هم میداند. باید عادت کنیم در تمام کارهای علمی، تکروی را کنار بگذاریم. شما آزمایش کنید، حتی اگر یک داستان را دو یا سه نفری با هم بخوانید و درباره آن بحث کنید، در مقایسه با مطالعه انفرادی چه نتیجههای شگفتانگیزی به دست میآورید. طبیعت کارگروهی ایجاب میکند که با بحث و انتقاد و خردهگیری همراه باشد و همین وضع، به سالمتر شدن رابطهی انسانی افراد و هم به عمیقتر شدن یادگیری دانش، کمک فراوان میکند.
و اما سفارش دوم من این است که در دانشآموزان، اعتماد به خود به وجود آورید. وقتی به کسی از چپ و راست، وصله بیشعوری و بیاستعدادی زده میشود، او به تدریج این اعتقاد دیگران را میپذیرد، اعتماد نسبت به خود را از دست میدهد و باور میکند که نمیتواند چیزی یاد بگیرد.
ادامه مطلب ...موفقیت ریاضی دانان ایرانی در حل یک مسأله
خدایا

خدایا برای این همه نعمت ازتو سپاسگزاریم.
ویژگی های عدد 6174
عدد 6174 را در نظر بگیرید و ارقام آن را چنان جابه جا کنید که بزرگترین عدد ممکن از آنها ساخته شود، یعنی آنها را به ترتیب نزولی قرار دهید. همچنین ارقام این عدد را طوری جابه جا کنید که کوچکترین عدد ممکن از آنها تشکیل شود و عدد اخیر را از عدد اول کم کنید خواهیم داشت: 6174 = 1467 - 7641 که همان عدد اول است.حال همین روش را برای عددی مثل 4959 اجرا می کنیم داریم :
5355 = 4599 - 9954
و همین طور برای 5355 داریم :
1998 = 3555 - 5553
و همین طور برای 1998 داریم :
8082 = 1899 - 9981
8532 = 0288 - 8820
6174 = 2358 - 8532
واقعیت این است که با هر عدد چهار رقمی این کار را شروع کنیم به شرط اینکه ارقام همگی یکسان نباشند، این روش عدد 6174 را در حداکثر 7 مرحله بدست خواهد داد.
سرفصلهای ریاضی اول متوسطه(پایه هفتم)جدید
فصل ۱:راهبردهای حل مسئله- روشهای نمادین
فصل 2: عددهای صحیح
فصل 3: هندسه و استدلال(رابطه بین پاره خط ها، رابطه بین زاویه ها، رسم مثلث، تساوی دو مثلث، مثلث قائم الزاویه)
فصل 4: جبر و معادله(الگوهای عددی، عبارت جبری، مقدار یک عبارت جبری، معادله)
فصل 5: مساحت و حجم (یادآوری، معرفی حجم های هندسی، حجم شکلهای هندسی، مساحت جانبی، سطح و حجم)
فصل 6: اعداد طبیعی و اعداد اول
فصل 7: بردار(پاره خط جهت دار، تعریف بردار، کاربرد بردار در نیرو و حرکت، مختصات، بردار و حرکت نقطه در صفحه، جمع دو بردار)
فصل 8: توان(معرفی توان، محاسبه عبارت توان دار، ساده کردن عبارت های توان دار، مفهوم جذر و ریشه)
فصل 9: احتمال (دسته بندی داده ها، مفهوم نمونه و جامعه، میانگین داده ها در حالت دسته بندی، مفهموم احتمال و پیشامد، تعداد حالت های ممکن، احتمال ریاضی)
فصل 10:اعداد گویا(معرفی اعداد گویا، جمع و تفریق، ضرب و تقسیم، عددهای گویا و گنگ مقایسه اعداد گویا و گنگ)
فصل 11:تبدیل های هندسی(خطوط موازی و مورب، تقارن و تجانس، عمود منصف و نیمساز،مفهوم تشابه)
