اصل استقراء تعمیم یافــته:

اصل استقراء تعمیم یافــته:
گاهی ممکن است با احکامی روبه رو شویم که برای n=1 برقرار نمی باشند و باید در بررسی شرط اول (مرحله مبنا) از عددی طبیعی بزرگتر استفاده کنیم به این ترتیب از اصل استقراء تعمیم یافــته استفاده می کنیم.

اصل استقرای تعمیم یافته:
اگر (P(nحکمی در باره اعداد طبیعی n (یا صحیح) باشد در صورتی که:
1- برای هر عدد طبیعی P(m) ، m>1 درست باشد
2- به ازای هر عدد طبیعی ، از درستی (P(k درستی (P(k+1 نتیجه شود
آنگاه میتوان گفت حکم (P(n برای هر عدد طبیعی برقرار است.

• به این ترتیب در اثبات مسائل به کمک اصل استقرای تعمیم یافته باید m مناسب را برای بررسی شرط اول بیابیم.

مثال: نشان دهید عدد طبیعی مناسبی مانند m وجود دارد که برای هر عدد طبیعی n بزرگتر یا مساوی m داریـم: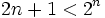

پاسخ: با قرار دادن مقادیر طبیعی برای m متوجه می شویم که m مناسب 3 است چرا که برای اولین بار حکم برای m=3 درست است. حال نشان میدهیم حکم برای هر عدد طبیعی 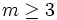برقرار است.
1-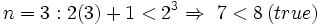
2- اکنون در این مرحله فرض (فرض استقرا) می کنیم نامساوی فوق برای هر عدد طبیعی درست باشد یعنی: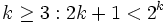
نشان میدهیم حکم داده شده برای (n=k+1 ،(k>2 درست است، یعنی: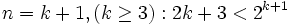
(حکم استقرا)
برای این منظور از فرض استقرا استفاده کرده و به طرفین فرض عدد 2 را اضافه می کنیم، داریم:

حال با مقایسه نامساوی اخیر و حکم استقرا کافی است نشان دهیم: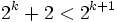

برای این کار از اثبات بازگشتی کمک میگیریم: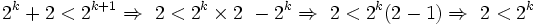


مشاهده می شود نامساوی 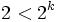برای K>2 همواره درست است و چون تمامی روابط برگشت پذیرند، لذا 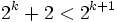برقرار بوده و به این ترتیب حکم برای هر عدد طبیعی 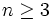برقرار اس