مثالی برای استقرای تعمیم یافته

مثال: نشان دهید در هر n ضلعی محدب تعداد قطرها برابر است با: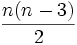

پاسخ: می دانیم یک 3 ضلعی محدب، مثلث دارای هیچ قطری نمی باشد و چهار ضلعی محدب دارای
دو قطر است. به این ترتیب حکم را برای n>3 اثبات می کنیم. مرحله اول (مبنا) را با n=4 آغاز می کنیم:
1-
حال فرض می کنیم که حکم برای n=k درست باشد، یعنی تعداد قطرهای هر k ضلعی محدب برابر باشد با:

نشان می دهیم که حکم برای n=k+1 هم درست است، یعنی تعداد قطرهای هر k+1 ضلعی محدب برابر است با:

برای اثبات سعی می کنی به گونه ای از فرض استقرا استفاده کنیم. به این صورت که می دانیم که اگر به تعداد ضلعهای یک n ضلعی، یک ضلع اضافه کنیم یا به تعداد رئوس آن یک راس اضافه کنیم به تعداد قطرهای آن n-1 واحد اضافه می شود. لذا:

(k-1)+تعداد قطرهای k ضلعی محدب=تعداد قطرهای k+1 ضلعی محدب

بنابراین رابطه زیر برقرار است:

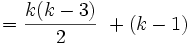تعداد قطرهای k+1 ضلعی محدب

و لذا حکم برای هر n>3 برقرار است.

اصل استقراء تعمیم یافــته:

اصل استقراء تعمیم یافــته:
گاهی ممکن است با احکامی روبه رو شویم که برای n=1 برقرار نمی باشند و باید در بررسی شرط اول (مرحله مبنا) از عددی طبیعی بزرگتر استفاده کنیم به این ترتیب از اصل استقراء تعمیم یافــته استفاده می کنیم.

اصل استقرای تعمیم یافته:
اگر (P(nحکمی در باره اعداد طبیعی n (یا صحیح) باشد در صورتی که:
1- برای هر عدد طبیعی P(m) ، m>1 درست باشد
2- به ازای هر عدد طبیعی ، از درستی (P(k درستی (P(k+1 نتیجه شود
آنگاه میتوان گفت حکم (P(n برای هر عدد طبیعی برقرار است.

• به این ترتیب در اثبات مسائل به کمک اصل استقرای تعمیم یافته باید m مناسب را برای بررسی شرط اول بیابیم.

مثالی برای استقرای ریاضی

مثال: نشان دهید برای هر عدد طبیعی n: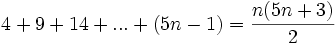

پاسخ: اثبات را با استفاده از اصل استقرای ریاضی انجام می دهیم:
1- درستی حکم داده شده را برای n=1 بررسی می کنیم: (مرحله مبنایی استقرا)
سمت راست تساوی: 4
سمت چپ تساوی: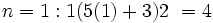
پس برای n=1 طرفین تساوی دادهشده با هم برابر می شوند که نشان می دهد حکم برای n=1 درست است.
2- فرض می کنیم تساوی داده شده به ازای عدد طبیعی n=k برقرار باشد(فرض استقرا) یعنی: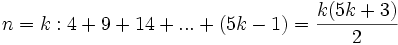

حال نشان میدهیم حکم برای n=k+1 هم برقرار است(حکم استقرا) یعنی: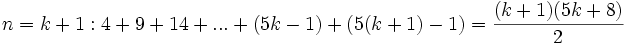

برای اثبات حکم استقرا از فرض استقرا کمک می گیریم. برای این کار به طرفین فرض استقرا عبارت 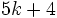را اضافه میکنیم: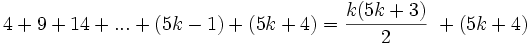

حال در سمت راست تساوی فوق داریم: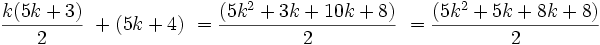


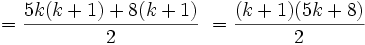
پس نشان داده شد: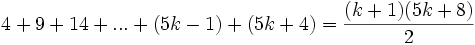
به این ترتیب بر طبق اصل استقرا حکم فوق برای هر n عضو اعداد طبیعی برقرار است.

اتحادها

اتحاد:

در ریاضیات اتحادها تساوی هایی هستند که به ازای هر مقدار عددی از دامنه خود که بجای متغییرهایشان قرار دهیم همواره برقرار باشند.
به عنوان مثال تساوی 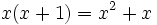برای هر x عضو دامنه برقرار است. لذا این عبارت جبری یک اتحاد است، اما تساوی 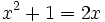فقط برای x=1 برقرار است. پس این عبارت یک اتحاد نمی باشد. در واقع در مورد یک اتحاد در اصل به یک تساوی بدیهی چون 0=0 می رسیم.
به عنوان مثال در اتحاد مثال زده شده 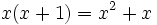دو طرف ساده شده و تساوی 0=0 حاصل می شود.
به این ترتیب تفاوت میان یک اتحاد جبری و یک معادله جبری در این است که اتحاد جبری به ازای همه مقادیر دامنه برقرار است در صورتی که یک معادله جبری به ازای تعداد محدودی از اعضای دامنه(مجموعه جواب معادله) برقرار است.
عبارات زیر نمونه ای از اتحاد است:

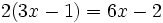
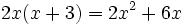
• اتحادهای مهم جبری:

در میان اتحادهای جبری، برخی از اتحادها بسیار مهم و کاربردی می باشند و در حل معادلات، محاسبات جبری، تجزیه عبارت جبری و... بسیار کاربرد دارند. از این رو دانستن و به کاربردن آنها از اهمیت خاصی برخوردار است. در این قسمت به بررسی این اتحادهای مهم می پردازیم:

• اتحاد مربع مجموع دو جمله:

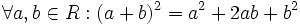
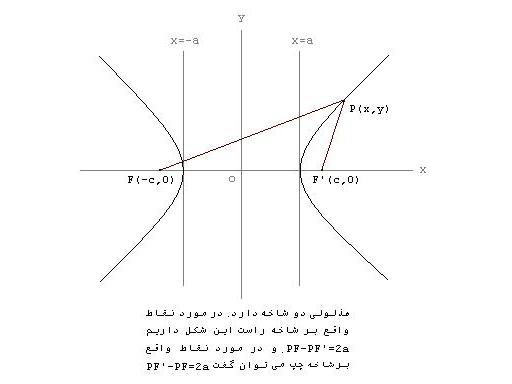
معادله هذلولی

معادله ی هذلولی

با در نظر گرفتن دو نقطه ی ثابت 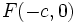و موسوم به کانون ها و مقدار ثابت 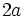، آن گاه نقطه ای چون بر هذلولی واقع است اگر و تنها اگر:

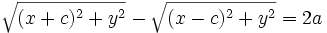
یا

معادله بیضی

معادله بیضی

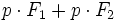اگر دو نقطه ثابت به نام کانون ها، نقاط و باشند و مجموع فاصله ها، ، با 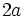نمایش داده شود، آنگاه مختصات نقطه ای چون واقع بر بیضی در معادله زیر صدق می کند :

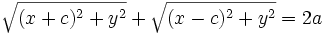
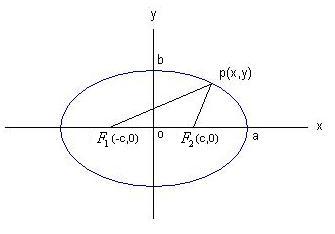
برای ساده کردن این معادله، رادیکال دوم را به سمت راست معادله برده، رابطه حاصل را به توان دو می رسانیم و پس از ساده کردن داریم :

تقسیم پذیری:

تقسیم پذیری:

نظریه بخش پذیری (یا همان تقسیم پذیری) از بخش های اصلی و آغازین نظریه اعداد است که بسیاری از قضایای نظریه اعداد در اثبات های خود از آن بهره می‌گیرند. معمولاً در نظریه مقدماتی اعداد، بخش پذیری را با الگوریتم تقسیم و رابطه عاد کردن شروع می‌کنند. الگوریتم تقسیم قضیه ای است که می‌گوید: به ازای هر دو عدد صحیح a و b که b≠0 اعداد صحیح و منحصر به فردی مانند q و r وجود دارند به طوری که:

a=b.q + r

همچنین به جای شرط بالا می‌توان از شرط « r<|b| » استفاده کرد که البته دیگر r و q در آن منحصر به فرد نیستند؛ یعنی اگر ما از شرط دوم اسفاده کنیم، صورت قضیه کمی فرق می‌کند و شرط منحصر به فرد بودن r و q از آن برداشته می‌شود. رابطه ی عاد کردن که با نماد «|» (یک پاره خط عمودی) نشان داده می‌شود، به صورت زیر تعریف می‌شود:

b|a اگر و تنها اگر برای k متعلق به اعداد صحیح a=b.k

در این صورت می‌گویند:

1. عدد b، عدد a را عاد می‌کند.
2. عدد b، عدد a را می‌شمارد.
3. عدد b، یک عامل عدد a است.
4. عدد aٰ، مضربی از عدد b است.

بدون شرح

بدون شرح

خدایا...

خدایا...چه بی حساب می بخشی وچه باحساب تسبیحت میگوییم...34مرتبه الله اکبر...33مرتبه الحمدلله...33مرتبه سبحان الله...

بیا مهدی شب هجران سحر کن

مهدی شب هجران سحر کن ...

9 ربیع الاول سالروز به امامت رسیدن

حضرت مهدی(عج) بر تمامی شیعیان مبارک باد

خدایا به ما توفیق عنایت بفرما که از منتظران واقعی باشیم

انشاالله

 

برگرفته شده ازوبلاگ ندای سحر

معادله جزء صحیح

معادله جزء صحیح

مجموعه جواب معادله جزء صحیح c[[x] - x] = 0 را بیابید.

روش اول

به ازای اعداد صحیح مثبت مثلا" 2 و c- 2 داریم

c[[2] - 2] = [2 - 2] = 0 ; [[-2] + 2] = [- 2 + 2] = 0

و به ازای اعداد غیر صحیح 2.5 و c- 2.5 داریم

c[[2.5] - 2.5] = [2 - 2.5] = -1 ; [[- 2.5] + 2.5] = [- 3 + 2.5] = -1

بنابراین تمام اعداد صحیح در مجموعه جواب هستند.

روش دوم

برای اینکه معادله c[[x] - x] = 0 همیشه صادق باشد باید همواره c0 =< [x] - x < 1 باشد.

با رسم نمودار تابع y = [x] - x دیده می شود که این تابع متناوب بوده و مقدار آن همواره بین صفر و منفی یک می باشد.

مثلا" در فاصله c0 =< x < 1 تابع برابر y = - x می باشد.

بنابراین معادله صورت مسئله فقط برای اعداد صحیح صادق است.

دامنه تابع لگاریتمی کسری

دامنه تابع لگاریتمی کسری

دامنه تابع زیر را بیابید. (y = log_x-1(x²-1) / log_x-1(x+1

اولا" اعداد منفی لگاریتم ندارند.

بنابراین باید

x + 1 >= 0 --> x >= -1
و
x² - 1 >= 0 --> x² >= 1 --> x >= 1 or x =< -1

ثانیا" لگاریتم در پایه منفی یا صفر یا یک تعریف نشده است.

بنابراین باید
x - 1> 0 --> x > 1

و
x - 1 # 1 --> x # 2

ثالثا" مخرج کسر نباید صفر شود.

بنابراین باید
x + 1 # 1 --> x # 0

در کل تمام شروط منتج می شود به
x > 1 and x # 2

محور تقارن تابع قدر مطلق

محور تقارن تابع قدر مطلق

اگر خط x = 2 محور تقارن تابع زیر باشد مقدار k چیست؟

y = |2x + 1| + |2x + k|c

با رسم نمودار تابع به سادگی دیده می شود که خط قائم x = -1/2 محور تقارن قسمت اول تابع و خط قائم x = - k/2 محور تقارن قسمت دوم تابع است.

بنابراین واسطه عددی این دو مقدار محور تقارن تابع اصلی می باشد.

بنابراین
c(-1/2 - k/2)/2 = 2 --> - k - 1 = - 8 --> k = 7

مماس بودن خط بر منحنی

مماس بودن خط بر منحنی

به ازای کدام مقدار b خط به معادله y = - 3x + b بر منحنی y = x³ - 3x² مماس است؟

نکته :در نقطه مماس اولا" y خط و منحنی و ثانیا" مشتق آن دو با هم برابرند.

بنابراین :

y₁' = - 3 , y₂' = 3x² - 6x ---> 3x² - 6x = - 3 ---> x² - 2x + 1 = 0
(x - 1)² = 0 ---> x = 1 , y = 1 - 3 = -2

بنابر این مختصات نقطه تماس طول 1 و عرض 2- است و این مختصات در معادله خط نیز صدق می کند .

بنابراین :

b - 3 = -2 و از آنجا b = 1

نقطه عطف

نقطه عطف

به ازای چه مقدار m نقطه عطف منحنی تابع زیر بر مبدا مختصات منطبق است ؟
y = mx³ - 2(m+1) x²

مشتق دوم تابع را محاسبه نموده و با صفر قرار دادن آن طول نقطه عطف را به دست می آوریم .

(y ' = 3mx² - 4(m+1)x --> y"= 6mx - 4(m +1

6mx - 4(m +1)= 0 --> x = 2(m+1)/3m

اما طبق صورت مسئله طول نقطه عطف صفر است .

بنابراین :
m+1)/3m = 0 --> m= -1 )٢

برای تست می توانیم مقادیر m= -1 و x= 0 را در تابع قرار داده و عرض نقطه عطف یعنی y= 0 را به دست آوریم .

تابع درجه دو

نمودار تابع درجه دوم

به ازای کدام مقدار m نمودار تابع با ضابطه y= (m - 2)x² - 3x+m+2 بالای محور x ها و مماس بر آن است ؟

اولا" برای اینکه نمودار تابع در بالای محور x ها باشد باید دهانه این نمودار سهمی رو به بالا بوده و بنابراین ضریب x² مثبت باشد.

m - 2 > 0 --> m>2

ثانیا" برای اینکه نمودار مماس بر محور x ها باشد باید تابع درجه دوم مفروض فقط یک ریشه داشته باشد یعنی دلتای آن صفر باشد.

b² - 4ac= 9 - 4(m -2).(m+2)= 0 --> m=⁺_- 2.5

با اشتراک دو شرط بالا فقط مقدار m=2.5 قابل قبول است

نقطه بحرانی

نقطه بحرانی:

نقاط بحرانی تابع f(x)= x^4/3 - x^2/3 در فاصله بسته 1- تا 1 کدامند؟

نکته : نقاطی که در آن مشتق تابع صفر شود ویا در آن نقاط مشتق وجود نداشته باشد و یا در آن نقاط مشتق بی نهایت شود نقاط بحرانی هستند.در ضمن نقاط دو سر بازه نیز نقاط بحرانی است.

بنابراین ابتدا مشتق تابع را می یابیم :

(f '(x)= (4/3)x^1/3 - (2/3)x^-1/3= (2/3)(2root³x - 1/root³x

و یا
f '(x)=2(2root³x² -1)/3root³x

توجه : منظور از root³x² ریشه سوم x² است.

دیده می شود که اولا" مشتق در x= 0 بی نهایت می شود و ثانیا" با صفر قرار دادن (f '(x داریم :

f '(x)= 0 --> 2root³x² =1 --> x²=1/8 --> x=⁺_- root2/4

بنابراین نقاط 0 و root2/4 و root2/4 - سه نقطه بحرانی تابع هستند.

قضیه مقدارمیانگین در مشتق:

قضیه مقدارمیانگین در مشتق:

تابع f با ضابطه f(x) = x²+x+1 در بازه بسته 1 تا a در نقطه c = 2 در قضیه مقدار میانگین برای مشتق صدق می کند. عدد a مربوط به این قضیه چیست؟

نکته : طبق قضیه مقدار میانگین در مشتق شیب خط مماس در c برابر شیب خط AB است.(بین x=1 و x= a )

ابتدا مقادیر تابع در این دو نقطه را می یابیم

f(1) = 3 , f(a) = a²+a+1

و شیب خط واصل بین این دو نقطه برابر است با

(m = (a²+a+1 - 3)/(a -1) = (a²+a - 2)/(a -1

سپس با مشتق گیری شیب خط مماس در نقطه c = 2 را می یابیم

f'(x) = 2x+1 --> f'(2) = 5

و در نتیجه
c (a²+a -2)/(a -1) = 5 --> a² - 4a+3 = 0

و یا
c (a - 3)(a -1) = 0 --> a =1 , a = 3

و طبیعی است که مقدار a = 3 قابل قبول است.

دو منحنی مماس:

دو منحنی مماس:

نمودارهای دو تابع با ضابطه های y = ax²+bx - 9 و y = x³/3 - 4x در نقطه ای به طول 3 مماس مشترک دارند. مقادیر a و b را بیابید.

نکته : دو منحنی مماس اولا" دارای نقطه تماس مشترک و ثانیا" دارای مماسهای برابر هستند.

بنابراین ابتدا در x = 3 دو مقدار تابع با هم برابرند

y₂ = y₁ --> x³/3 - 4x = ax²+bx - 9

و در نتیجه
9a+3b - 9 = 9 - 12 --> 3a+b = 2

و مساوی بودن مشتقها در همین نقطه

y₁' = y₂' --> 2ax+b = x² - 4

و در نتیجه
6a+b = 9 - 4 --> 6a+b = 5

و با حل دستگاه دو معادله دو مجهولی داریم

a = 1 , b = -1

خط قائم بر منحنی

خط قائم بر منحنی:

تعداد قائمهایی که از نقطه A(3,0)c بر منحنی تابع y² = 4x می توان رسم کرد چند تاست؟

نقطه A خارج منحنی است.

اگر عرض نقطه برخورد قائم را a فرض کنیم طول آن a²/4 خواهد بود.

و شیب خط قائم برابر است با

m' = (y₂ - y₁)/(x₂ - x₁) = (a - 0)/(a2/4 - 3)c

و یا
m' = 4a/(a² -12)c

از طرف دیگر با گرفتن مشتق از تابع نیز می توان این شیب را حساب کرد

2yy' = 4 --> y' = 2/y --> m = 2/a --> m' = - a/2

و با برابر قرار دادن این دو شیب داریم

4a/(a² -12) = - a/2 --> a³ - 4a = 0

و یا
a(a² - 4) = 0 --> a = 0 ; a = 2 ; a = - 2

بنابراین سه قائم می توان رسم کرد.