علم ریاضی

این وبلاگ جهت استفاده علاقمندان به ریاضی ایجاد شده است.

علم ریاضی

این وبلاگ جهت استفاده علاقمندان به ریاضی ایجاد شده است.

ویژگی قدرمطلق

ویژگیهای قدر مطلق:

برای هر عدد حقیقی a قدر مطلق a که آن را با |a| نمایش می‌دهیم به صورت زیر تعریف می‌شود:

$|a| = \begin{cases} a, & \mbox{if} a > 0 \\ -a, & \mbox{if} a < 0. \end{cases}$

همان گونه که در بالا نشان داده شده‌است قدر مطلق یک عدد همواره صفر یا مثبت است و هرگز منفی نیست.

در هندسه تحیلی قدر مطلق یک عدد حقیقی برابر است با فاصله آن تا صفر بر روی یک خط حقیقی؛ در حالت کلی قدر مطلق تفاضل دو عدد برابر است با فاصلهٔ میان آن دو عدد. در واقع می‌توان گفت که مفهوم تابع فاصله در ریاضی همان قدر مطلق تفاضل است که در حالت کلی بیان شده‌است.

ریشه دوم یک عدد را می‌توان به صورت زیر نشان داد:

$|a| = \sqrt{a^2}$

$(1)$

که گاهی از آن به عنوان تعریف قدر مطلق استفاده می‌شود.

چهار ویژگی اصلی قدر مطلق عبارتند از:

$\|a\| \ge 0$	$(2)$	نا صفر بودن
$\|a\| = 0 \iff a = 0$	$(3)$	صفر بودن
$\|ab\| = \|a\|\|b\|\,$	$(4)$	ضرب‌پذیری
$\|a+b\| \le \|a\| + \|b\|$	$(5)$	جمع‌پذیری

دیگر ویژگی‌های آن عبارتند از:

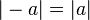
$\|-a\| = \|a\|\,$	$(6)$	تقارن
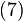
$\|a - b\| = 0 \iff a = b$	$(7)$	گرفته شده از صفر بودن
$\|a - b\| \le \|a - c\| +\|c - b\|$	$(8)$	نامساوی مثلث گرفته شده از جمع‌پذیری
$\|a/b\| = \|a\| / \|b\| \mbox{ (if} b \ne 0) \,$	$(9)$	تقسیم پذیری گرفته شده از ضرب‌پذیری
$\|a-b\| \ge \|\|a\| - \|b\|\|$	$(10)$

اگر فرض کنیم که b > ۰ است آنگاه دو ویژگی دیگر قدر مطلق می‌توان چنین نوشت:

$|a| \le b \iff -b \le a \le b$

$|a| \ge b \iff a \le -b \mbox{ or} b \le a$

از این ویژگی‌ها می‌توان در حل نامساوی‌ها استفاده کرد؛ برای نمونه:

$\|x-3\| \le 9$	$\iff -9 \le x-3 \le 9$
	$\iff -6 \le x \le 12$

از قدر مطلق دز تعیین فاصله مطلق در سامانهٔ متری در مجموعه اعداد حقیقی استفاده می‌شود.

تابع‌های قدر مطلق

تابع حقیقی قدر مطلق در همه جا پیوسته است و در همه جا به جز نقطهٔ x = ۰ مشتق‌پذیر است. این تابع در بازهٔ [۰ ∞-) اکیدا نزولی و در بازهٔ (∞+ ۰] اکیدا صعودی است و چون قدر مطلق عدد مثبت و منفی با هم برابر است پس تابعی زوج است و وارون ناپذیر.

در تابع حقیقی قدر مطلق، تابع مرکب خود آن‌ به صورت 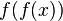$f(f(x))$ با خود تابع 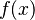$f(x)$ برابر است.

مشتق تابع قدر مطلق

مشتق تابع قدر مطلق حقیقی برابر است با تابع علامت که با نماد sgn نمایش داده می‌شود، تابع زیر تنها به ازای x‌های ناصفر تعریف شده‌است:

$\sgn (x) = \frac{x}{|x|},$

تابع قدر مطلق حقیقی در x = ۰ مشتق‌پذیر نیست.
یادآوری: تابع علامت تابعی است که بدون توجه به مقدار x تنها علامت x را نشان می‌دهد بنابراین می‌توان گفت که $x = sgn(x)abs(x)$

سهراب .غفاری یکشنبه 25 فروردین‌ماه سال 1392 ساعت 08:33 ق.ظ

نظرات 4 + ارسال نظر

سینا لطفعلی جمعه 18 دی‌ماه سال 1394 ساعت 08:46 ب.ظ

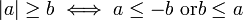
میشه اثباتش رو هم بزارین ؟ :/

فرشته یکشنبه 21 مرداد‌ماه سال 1397 ساعت 08:19 ب.ظ

حسین آقا جمعه 20 دی‌ماه سال 1398 ساعت 11:16 ب.ظ

کاظم توتونچی جمعه 22 مرداد‌ماه سال 1400 ساعت 10:00 ب.ظ

لطفا کتاب فارسی یا زبان اصلی برای اثبات ها وجود داره برای ایمل بنده ارسال کنید.
زحمت کشیدین و قوانین در سایت گذاشتید . لطفا اثبات هاا راهم قرار بدهیید برای درک بهتر