عدد بعدی کدام است ؟

عدد بعدی کدام است ؟ 

 

…. ، ۵۵ ، ۱۹ ، ۷ ، ۳

الف) ۱۷۳       ب) ۱۴۳           ج) ۱۵۳            د) ۱۶۳

بیست نکته در آموزش ریاضی

دانش آموزان عزیز برای آنکه بتوانید ریاضی را بهتر بخوانید، بهتر بفهمید، بهتر یاد بگیرید و بیشتر با آن دوست شوید بیست نکته زیر را بخوانید و به کار ببرید:

۱-به خاطر داشته باشید که یادگیری درس ریاضی حتما باید در کلاس انجام گیرد زیرا یادگیری این درس به شدت وابسته به معلم است.

۲- برای یادگرفتن ریاضیات داشتن تمرکز الزامی است. پس به هنگام یادگیری سر تا پا گوش باشید. به ویژه اینکه دبیر ریاضی از معدود دبیران پشت به کلاس است زیرا دائما مجبور به استفاده از تخته برای نوشتن است.

 ۳- به توضیحات دبیر یا مدرس ریاضی باید کاملا دقت کنید زیرا چکیده ی چند سال تجربه و انتقال مطلب به همراه منطبق ریاضیاتی درس را تواما ارائه می کند.

۴- مراحل محاسباتی هر تمرین را به زبان خودتان برای خودتان بازگویی کنید و راهنما و خود آموز خاص خودتان را در هر مبحث بنویسید.

۵- از عدم توانایی یا مهارتتان در حل تمرینها و مسائل نترسید و دلسرد نشوید بلکه با شعف تمام با آن برخورد کنید زیرا با پی بردن به ضعف ها و نقص هایتان نیمی از عیب را رفع کرده اید.

۶- به هنگام حل تمرین حدس بزنید که چگونه سؤال یا سؤالات مشابهی ممکن است در امتحان بیابید.

۷- در انجام تمرینهای هندسه، درک این که قضیه از شما چه چیزی را می خواهد، مهم است. هر چه راههای بیشتر و جدیدتری برای بیان محتوای قضایا، تعاریف و اصول موضوعه پیدا کنید، هندسه را بهتر فهمیده اید.

۸- ریاضی سیری پلکانی دارد.بنابراین آمادگی مهارتی در انجام مفاهیم قبلا آموخته شده و درک آنها پیش نیاز درک مفاهیم ریاضی بعدی است.

۹- در کلاس درس ریاضی فعال باشید.دقت کنید، سؤال کنید تمرین کنید، مراحل محاسباتی را ثبت کنید.

۱۰-موقع یادگیری تلاش کنید ساختار ریاضی، ارتباطات، روابط اجزاء و منطبق ریاضی حاکم بر آن، کاربردها و سایر ویژگی های نظری مطلب را بفهمید.

۱۱- با خودسنجی در تمرین های ریاضی، بلافاصله علل ناکامی و عدم موفقیت خودتان در مقابله با تمرین را ریشه یابی کنید مثلا این ناکامی ناشی از این باشد که:

الف) در درک و فهم ریاضیاتی تمرین مورد نظر مشکل دارید.

ب) در حل تمرین یا تمرین های مورد نظر مشکل دارید.

ج) تمرین هایی که انجام داده اید به حد کفایت و لازم نبوده است.

۱۲- تمرین های ریاضی را یک ضرورت و نه اجبار تلقی کنید و با داشتن نگرش مثبت به این تکالیف و هدفمند بودن از تمرین های ریاضی استفاده بیشتری ببرید.

۱۳- فقط به تمرین های موجود در کتاب درسی بسنده نکنید بلکه از کتاب های ویژه حل تمرین یا به اصطلاح کتاب کار هم استفاده کنید.

۱۴- اصل اساسی در انجام تمرین های ریاضی استفاده از استدلال قیاسی است نسبت به این مساله حساس و واقف باشید تا سرعت کارتان زیاد شود.

۱۵- هیچ گاه به هنگام خستگی به ادامه تمرین ریاضی نپردازید زیرا خستگی باعث کاهش دقت و تمرکزتان شده و ضریب خطاها و ناکامیتان را بالا می برد.

۱۶- ریاضی مثل هر علم دیگری زبان خاص خودش را دارد. این زبان را بفهمید و بیاموزید تا از ارتباط با ریاضی لذت بیشتری ببرید. زبان ریاضی مجموعه ای از اعداد، علائم و نمادها، حروف، اشکال و روابط بین آنهاست.

۱۷- یکی از موانع درک ریاضی، نداشتن تصور ریاضیاتی مثبت از خود است. این موانع ممکن است در درک ریاضی، در تمرین ریاضی، در امتحان ریاضی دادن یا در تست ریاضی زدن باشد. با تلاش و تمرین سعی کنید بر این موانع غلبه کنید.

۱۸-اصول حل مساله را یاد بگیرید و به کار ببرید. این اصول شامل موارد زیر است:

۱) مساله را بفهمید. یعنی فرض ها و شروط مسأله را درک کنید. داده ها و مجهول ها را روی کاغذ بیاورید، ترسیم کنید یا مجسم کنید.

۲) ارتباط منطقی میان داده ها، شروط مسأله و مجهول را پیدا کنید.

۳) راه حل ها را پیدا کنید.

۴) عملیات را اجرا کنید و محاسبات لازم را انجام دهید.

۵) جوابهای به دست آمده را وارسی کنید و از صحت آنها مطمئن شوید.

۶) راه حل های کوتاه تر یا متفاوت را پیدا کنید.

۱۹- هرگز قبل از حصول اطمینان از یادگیری متن و جوهره ی درس به سراغ انجام تمرین نروید زیرا احتمال ناکام شدن و عدم موفقیت تان زیاد خواهد بود.

۲۰- هرگز به سراغ حل المسائل نروید مگر آنکه قبلا:

۱-کتاب درسی را خوانده باشید.

۲-جزوه درسی تان را دقیق مطالعه کرده باشید.

۳-از کتاب کمک درسی یا نوار یا سی دی آموزشی استفاده کرده باشید.

۴-از معلم تان برای رفع اشکال کمک گرفته باشید.

۵-به دوستانتان یا همکلاسی های برتر برای رفع اشکال مراجعه کرده باشید.

۶-از اعضاء خانواده یا دیگران کمک گرفته باشید

هفت سین ریاضی

تبریک سال نو

فرخنده باد بر همگان مقدم بهار                نوروز ، جاودانه‌ترین جشن روزگار 

کمی تامل

درکلاس درس ریاضی سال سوم تجربی سوال زیر توسط دانش آموزی به صورت زیر نتیجه گیری شده: 

ثابت کنید :   4=5 

فرض میکنیم:0=20-20    

        0=25-25  چون طرفهای دوم برابرند پس طرفهای اول نیز برابر میشوندپس:25-25=20-20 

        حال ازطرفین فاکتورمی گیریم.   5  (5-5)=4(5-5)     حال دوطرف تساوی رابر مقدار مساوی 5-5 تقسیم میکنیم. 

       وازآنجا نتیجه میشود4=5  

ایراد این نتیجه گیری اینست که فقط طرفین تساوی را برعددغیرصفر می توان تقسیم کرد درحال که دراین مسله  

طرفین برعدد صفر یعنی 5-5 تقسیم کردیم.    

دنباله مثلثی

عدد مثلثی

یک عدد مثلثی برابر تعداد نقاط موجود در یک شبکه‌ی مثلثی است که در سطر اول آن یک نقطه وجود دارد و سطرهای دیگر آن هریک، یک نقطه بیش‌تر از سطر قبلی خود دارند.

به‌طور مثال

همان‌گونه که در شکل 1 مشاهده می‌کنید اعداد 1،3،6،10، 15 و 21 اعداد مثلثی هستند.

شکل 1.

به‌عبارت دیگر امین عدد مثلثی معادل است با مجموع اعداد طبیعی 1 تا  که مقدار این عدد معادل  خواهد بود.

اعداد مثلثی خواص جالبی دارند.

به‌طور مثال

مجموع دو عدد مثلثی متوالی یک «عدد مربع» است. در واقع مجموع دو عدد مثلثی متوالی برابر مربع اختلاف‌شان است.

این واقعیت را می‌توان در شکل 2 به‌طور شهودی دید.

شکل 2.

دنباله ی اعداد فیبوناچی

در دوران حیات فیبوناچی مسابقات ریاضی در اروپا بسیار مرسوم بود در یکی از همین مسابقات که در سال ۱۲۲۵ در شهر پیزا توسط امپراتور فردریک دوم برگزار شده بود مسئله زیر مطرح شد:

«فرض کنیم خرگوش‌هایی وجود دارند که هر جفت (یک نر و یک ماده) از آنها که به سن ۱ ماهگی رسیده باشند به ازاء هر ماه که از زندگی‌شان سپری شود یک جفت خرگوش متولد می‌کنند که آنها هم از همین قاعده پیروی می‌کنند حال اگر فرض کنیم این خرگوشها هرگز نمی‌میرند و در آغاز یک جفت از این نوع خرگوش در اختیار داشته باشیم که به تازگی متولد شده‌اند حساب کنید پس از n ماه چند جفت از این نوع خرگوش خواهیم داشت.»

حال اگر تعداد خرگوش ها را در ماههای اول و دوم و ... حساب کنیم به دنباله زیر خواهیم رسید که به دنباله فیبوناچی مشهور است.

۱, ۱, ۲, ۳, ۵, ۸, ۱۳, ۲۱, ۳۴, ۵۵, ۸۹, ۱۴۴, ۲۳۳, ۳۷۷, ۶۱۰, ۹۸۷, ۱۵۹۷, ۲۵۸۴,…

فیبوناچی با حل این مسئله از راه حل فوق دنباله حاصل را به جهان ریاضیات معرفی کرد که خواص شگفت‌انگیز و کاربردهای فراوان آن تا به امروز نه تنها نظر ریاضی‌دانان بلکه دانشمندان بسیاری از رشته‌های دیگر را به خود جلب کرده است.

برخی از خواص دنباله فیبوناچی:

مقدار خاصی که بستگی نزدیکی به دنباله فیبوناچی دارد، نسبت طلایی نامیده می‌شود. اگر هر عدد در دنباله فیبوناچی را به عدد پیش از خود تقسیم کنیم، مقدار این نسبتها بتدریج به یک عدد ثابت نزدیک می‌شود. یونانیان قدیم با این نسبت به خوبی آشنا بودند. معبد معروف پارتنون بهترین مثال از کاربرد این نسبت است. نسبت عرض به طول پنجره‌های مستطیل شکل معبد همگی برابر نسبت طلایی است. در اهرام مصر نیز این نسبت بخوبی رعایت شده است. طول هر ضلع قاعده هرکدام از اهرام به ارتفاع آن، معادل نسبت طلایی می‌باشد. این نسبت در آناتومی بدن انسان نیز بکار رفته است. اگر قد خود را بر فاصله عمودی ناف تا نوک انگشتان خود تقسیم کنید، تقریبا عدد 1.618 را بدست می‌آورید. با تقسیم طول بازوی خود از نوک انگشت بزرگ تا بالای شانه، بر فاصله نوک انگشت بزرگ تا آرنج خود نیز به این نسبت می‌رسید. از آنجایی که این نسبت در بسیاری از اندازه‌های بدن انسان وجود دارد، از آن به نام نسبت الهی نیز یاد می‌شود.

نسبت طلایی حضور خیره کننده‌ای در هندسه دارد. برای مثال این عدد برابر است با نسبت ضلع  یک پنج ضلعی منظم به طول قطر آن. اگر تمام قطرهای یک پنج ضلعی منتظم را بکشیم،‌ یک ستاره پنج پر بدست می‌آید که علامت بسیاری از پرچم‌های دنیاست.

نسبت طلایی در طبیعت نیز بچشم می‌خورد. تعداد گلبرگ‌های گلها اغلب برابر با یکی از اعداد فیبوناچی است.تعداد مارپیچ‌های گل آفتاب‌گردان نیز برابر با یکی از اعداد فیبوناچی است. این الگو را می‌توان در گلبرگ‌ها یا دانه های بسیاری از گیاهان مثلاً آناناس، گل داوودی، گل کلم، میوه های کاج و ... مشاهده کرد. شاید دلیل آن این باشد که وقتی دانه‌ها ( یا گلبرگ‌ها ) به این صورت قرار گیرند، بدون توجه به اندازه شان به طور یکنواخت و فشرده در کنار هم جا می‌گیرند؛ یعنی با اینکه عده ای از دانه‌ها کوچک تر از بقیه هستند، در هیچ ناحیه ای تراکم تغییر نمی کند و فضای خالی دیده نمی شود.

این خواص شگفت انگیز باعث شده است تا برخی، اعداد فیبوناچی را حامل رمزهای پنهان طبیعت بدانند.

 شگفتی ریاضی درطبیعت

ترس ازریاضی

در یک آزمایش جدید معلوم شد که ترس از ریاضیات می‌تواند شبکه‌های درد را در مغز فعال کند.

به گزارش ایسنا، متخصصان علوم پزشکی دانشگاه شیکاگو در این آزمایشات دریافته‌اند اضطراب ناشی از کلنجار رفتن با ریاضیات می‌تواند مناطقی را در مغز فعال کند که با تجربه به احساس دردهای جسمی و تشخیص تهدید غریزی، مرتبط هستند.

به گزارش سایت اینترنتی فیزورگ، این مطالعه به سرپرستی دکتر یان لیونز نشان داد در افرادی که هنگام مواجهه با مسائل ریاضی اضطراب شدیدی را تجربه می‌کنند، مناطقی از مغز که با احساس درد فیزیکی ارتباط دارند به فعالیت می‌افتند و هرچه این اضطراب و دلشوره بیشتر باشد این فعالیت عصبی نیز شدیدتر می‌شود و بنابراین احساس درد افزایش می‌یابد.

این متخصصان در بیانیه‌ای یادآور شدند: ما در این آزمایشات اولین مدرک عصبی را ارائه کرده‌ایم که نشان‌دهنده طبیعت تجربه فیزیکی مرتبط با ترس از ریاضیات است.

در مطالعات قبلی نیز نشان داده شده بود که سایر انواع استرس‌های روانی مانند انزوای اجتماعی و یا شکست عاطفی نیز می‌توانند احساس دردهای جسمی را در انسان بروز دهند اما در مطالعه جدید درواقع برای اولین بار واکنش درد مرتبط با حضور در یک موقعیت ایجاد اضطراب به جای خود حادثه استرس‌زا، آزمایش شده است.

در این آزمایش معلوم شد که حتی حضور در یک موقعیت ناخوشایند و نگران‌ کننده نیز پیش از اینکه حادثه‌ای رخ بدهد می‌تواند مناطق عصبی را با ایجاد درد جسمی ارتباط داده‌اند را فعال سازد و عملا احساس درد بدنی در انسان بوجود آورد.

این مطالعه در مجله پلوس وان منتشر شده است.

قضیه ساندویچ یا فشردگی

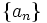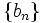اگر و و سه دنباله باشند به طوری که برای هر n طبیعی، داشته باشیم 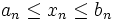و نیز آنگاه:

برهان: برطبق فرض چون 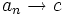داریم:

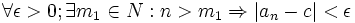
همچنین چون 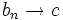داریم:

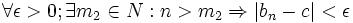
حال با فرض 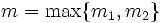برای هر n>m داریم:

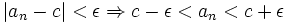
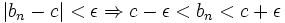
و چون بنا به فرض 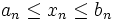پس:

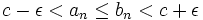
و لذا 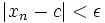که این نشان می‌دهد:

• نتیجه: اگر 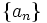دنباله‌ای کراندار و دنباله 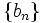به صفر همگرا باشد آنگاه:

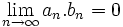
برهان:
برطبق فرض چون 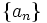کراندار است پس عددی چون k وجود دارد که برای هر n طبیعی داشته باشیم 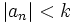پس:

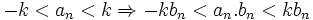
اما از طرفی 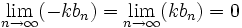پس بنا بر قضیه ساندویچ داریم:

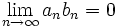
تعریف دنباله

دنباله (sequence) تابعی است که دامنه آن مجموعه اعداد طبیعی یا قطعه ای از مجموعه اعداد طبیعی باشد. پس در حالت کلی یک دنباله چون f تابعی است از مجموعه اعداد طبیعی به یک مجموعه دیگر چون A.

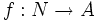
اگر دامنه دنباله قطعه ای از مجموعه اعداد طبیعی باشد دنباله را متناهی می‌گوییم و اگر دامنه دنباله خود مجموعه اعداد طبیعی باشد دنباله را نامتناهی می‌گوییم. به عنوان مثال دنباله اعداد طبیعی زوج کوچکتر از 10 یک دنباله متناهی است چرا که دامنه آن قطعه ای از مجموعه اعداد طبیعی یعنی 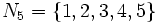است و دنباله اعداد زوج دنباله‌ای نامتناهی است چرا که دامنه آن خود مجموعه اعداد طبیعی است.

برای مشخص کردن یک دنباله مانند هر تابع دیگر باشد دامنه و ضابطه آن را مشخص کرد. ضابطه یک دنباله را در اصطلاح جمله عمومی آن دنباله می‌گوییم. اگر f یک دنباله باشد جمله عمومی آن را با (f(n و یا به صورتی معمول‌تر به صورت 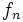نشان می‌دهیم. پس برای نمایش مقدار دنباله f به ازای عدد طبیعی n بجای نماد (f(n معمولا از نماد 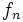استفاده می‌کنیم. به عنوان مثال در دنباله اعداد طبیعی زوج داریم:
برای نمایش خود دنباله از نماد استفاده می‌کنیم. پس دنباله اعداد طبیعی زوج را به این صورت نشان می دهیم:

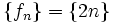
کشف قدیمی ترین سند ریاضی جهان

قدیمی ترین سند ریاضی جهان کشف شد!

 محققان موفق به کشف سند ریاضی با قدمت بیش از 2200 سال شده‌اند که قدیمی‌ترین نمونه کشف شده در چین محسوب می‌شود.  

 این سند باستانی ریاضی بر روی یک ورقه بامبو نوشته شده و قدمت آن به سال‌های 221 - 475  پیش از میلاد باز می‌گردد. 

 بر اساس اعلام مرکز تحقیقات و حفاظت از متون کاوش‌های باستانی دانشگاه چینهوا، در این سند ریاضی روش ضرب دو عدد زیر 100 توضیح داده شده است.

 توایع محاسباتی در این سند باستانی، بیشتر و قدیمی‌تر از نمونه‌های کشف شده تاکنون است که برای آن مقطع زمانی، نمونه بسیار پیشرفته‌ای محسوب می‌شود.

 محققان این کشف را یک دستاورد مهم برای تاریخچه علم ریاضی چین و حتی جهان عنوان می‌کنند.  

 منبع:isna

میلاد پیامبر

  

چراغ دین ابوالقاسم محمد           رسول خاتم ویاسین واحمد 

میلاد پیامبر

میلاد پیامبر بزرگ اسلام حضرت محمد (ص) وامام جعفرصادق(ع) مبارک باد

کاش های ریاضیدانان

 

کاش مختصات کردارمان روی ربع اول همانطور می ماند و به سمت

ربع های دیگر نمی رفتیم.

ریاضیات مالی دریچه ای به رفتار انسان

نگارنده: محمد جلوداری ممقانی

ریاضیات مالی شاخه ای از ریاضیات است که برای جریان های پول و سرمایه در بازار های مالی مدل های ریاضی طراحی و مطالعه می نماید . حاصل این تحقیقات در تصمیم گیری دولت ها و بازیگران بازار منعکس می گردد.
بازار های مالی محل خرید و فروش دارایی ها هستند. بنابراین با توجه به تنوع دارایی ها ، در این بازار ها کارهای بسیاری صورت می پذیرد. از جمله : قیمت گذاری دارایی ها ، تسهیم دارایی ها ، بیمه ، وام و اعتبارات ، سرمایه گذاری ، عرضه اوراق بهادار و اوراق قرضه ، اختیارات معامله و غیره .
در این بازار ها نیز عامل تصادف از طریق انسان ها و گذشت زمان وارد و بر روند قیمت ها اثر می گذارد. بنا براین در مدل های ریاضی باید این عامل منظور شود.
با توجه به این که ویژگی گذشت زمان برای تمام بازیگران بازار یکسان و تغییرات قیمت ها مورد توجه آنان است ، مدل های مذکور مسایل مقدار اولیه تصادفی با متغیر زمان اند.
این مسایل در ساده ترین صورت از یک معادله ی دیفرانسیل تصادفی و یک شرط اولیه تشکیل شده اند.
رابطه ی محکمی بین مسایل مقدار اولیه ی تصادفی و معادلات انتگرال وجود دارد. بنابراین در ریاضیات مالی مفهوم انتگرال تصادفی نقش ویژه ای ایفا می نماید.
با اندکی تسامح می توان گفت که انتگرال های تصادفی ، انتگرال یک فرایند تصادفی نسبت به یک فرایند تصادفی دیگر است . اگر انتگرال ده یک فرایند حرکت براونی باشد (باز هم با اندکی تسامح) انتگرال را انتگرال ایتو می نامیم.
اکنون می توان ملاحظه کرد که ریاضیات مالی ترکیبی از اقتصاد ، فرایند های تصادفی ، آنالیز ریاضی (معادلات دیفرانسیل معمولی و معادلات دیفرانسیل با مشتقات جزیی) و نظریه اندازه و نظریه ی احتمال است.

اندکی تامل

انسان تمام خوبیها را با یک بدی فراموش میکند ؛

ولی خدا تمام بدیها را با یک خوبی فراموش میکند...

                  

راز موفقیت از زبان بزرگان

پایداری زندگی به برنامه‌ریزی درست و وسیله‌ی رسیدن به آن، مدیریت صحیح است. (حضرت علی (ع))

باید بخواهیم تا بتوانیم. (رنه دکارت)

کوشش، اولین وظیفه‌ی انسان است. (گوته)

دنیا به امید برپاست و انسان به امید زنده. (علی‌اکبر دهخدا)

به توانایی خود ایمان داشتن، نیمی از کامیابی است. (ژان ژاک روسو)

بهترین واقعه‌ی زندگی هنگامی است که آدمی خود را می‌شناسد. (تولستوی)

تمام موفقیت خود را مدیون تفکر منظم و یادداشت‌برداری دقیق هستم. (ادیسون)

تا ایمان، امید و سخت‌کوشی نباشد، هیچ کاری را نمی‌توان انجام داد. (هلن کلر)

از دیروز بیاموز، برای امروز زندگی کن و امید به فردا داشته باش. (آلبرت اینشتین)

وارد عمل شدن بدون برنامه‌ریزی، علت همه‌ی شکست‌هاست.(آلکس مک‌کنزی)

خلق گل‌های زیبا با معادلات پیچیده ریاضی

خلق گل‌های زیبا با معادلات پیچیده ریاضی

 یک هنرمند معلول با تلفیق تخیلات خود با معادلات پیچیده ریاضی، تصاویر زیبایی از گل‌ها و شکوفه‌ها خلق کرده است که در دنیای واقعی مشابهی ندارند.

  «دانیل بروان» هنرمند انگلیسی، کار طراحی این مجموعه گل را با استفاده از فناوری‌های پیشرفته انیمیشن رایانه‌یی از سال 2000 میلادی آغاز کرد، اما سه سال بعد در اثر یک سانحه دچار قطع نخاع از گردن به پایین شد.

 این هنرمند برای ادامه دادن به فعالیت هنری خود از «ونت ورث تامپسون» زیست شناس و ریاضیدان اسکاتلندی الهام گرفت که برای توضیح مسائل زیست شناسی از رسم و نمودارهای موجود در ریاضیات استفاده می‌کرد.

 با استفاده از یک رایانه که با شرایط جدید معلولیت وی تنظیم شده بود، «بروان» کار طراحی مجموعه گل را ادامه داد.

اربعین حسینی

 

اربعین سالارشهیدان تسلیت باد.