دامنه تابع لگاریتمی کسری

دامنه تابع لگاریتمی کسری

دامنه تابع زیر را بیابید. (y = log_x-1(x²-1) / log_x-1(x+1

اولا" اعداد منفی لگاریتم ندارند.

بنابراین باید

x + 1 >= 0 --> x >= -1
و
x² - 1 >= 0 --> x² >= 1 --> x >= 1 or x =< -1

ثانیا" لگاریتم در پایه منفی یا صفر یا یک تعریف نشده است.

بنابراین باید
x - 1> 0 --> x > 1

و
x - 1 # 1 --> x # 2

ثالثا" مخرج کسر نباید صفر شود.

بنابراین باید
x + 1 # 1 --> x # 0

در کل تمام شروط منتج می شود به
x > 1 and x # 2

محور تقارن تابع قدر مطلق

محور تقارن تابع قدر مطلق

اگر خط x = 2 محور تقارن تابع زیر باشد مقدار k چیست؟

y = |2x + 1| + |2x + k|c

با رسم نمودار تابع به سادگی دیده می شود که خط قائم x = -1/2 محور تقارن قسمت اول تابع و خط قائم x = - k/2 محور تقارن قسمت دوم تابع است.

بنابراین واسطه عددی این دو مقدار محور تقارن تابع اصلی می باشد.

بنابراین
c(-1/2 - k/2)/2 = 2 --> - k - 1 = - 8 --> k = 7

مماس بودن خط بر منحنی

مماس بودن خط بر منحنی

به ازای کدام مقدار b خط به معادله y = - 3x + b بر منحنی y = x³ - 3x² مماس است؟

نکته :در نقطه مماس اولا" y خط و منحنی و ثانیا" مشتق آن دو با هم برابرند.

بنابراین :

y₁' = - 3 , y₂' = 3x² - 6x ---> 3x² - 6x = - 3 ---> x² - 2x + 1 = 0
(x - 1)² = 0 ---> x = 1 , y = 1 - 3 = -2

بنابر این مختصات نقطه تماس طول 1 و عرض 2- است و این مختصات در معادله خط نیز صدق می کند .

بنابراین :

b - 3 = -2 و از آنجا b = 1

نقطه عطف

نقطه عطف

به ازای چه مقدار m نقطه عطف منحنی تابع زیر بر مبدا مختصات منطبق است ؟
y = mx³ - 2(m+1) x²

مشتق دوم تابع را محاسبه نموده و با صفر قرار دادن آن طول نقطه عطف را به دست می آوریم .

(y ' = 3mx² - 4(m+1)x --> y"= 6mx - 4(m +1

6mx - 4(m +1)= 0 --> x = 2(m+1)/3m

اما طبق صورت مسئله طول نقطه عطف صفر است .

بنابراین :
m+1)/3m = 0 --> m= -1 )٢

برای تست می توانیم مقادیر m= -1 و x= 0 را در تابع قرار داده و عرض نقطه عطف یعنی y= 0 را به دست آوریم .

تابع درجه دو

نمودار تابع درجه دوم

به ازای کدام مقدار m نمودار تابع با ضابطه y= (m - 2)x² - 3x+m+2 بالای محور x ها و مماس بر آن است ؟

اولا" برای اینکه نمودار تابع در بالای محور x ها باشد باید دهانه این نمودار سهمی رو به بالا بوده و بنابراین ضریب x² مثبت باشد.

m - 2 > 0 --> m>2

ثانیا" برای اینکه نمودار مماس بر محور x ها باشد باید تابع درجه دوم مفروض فقط یک ریشه داشته باشد یعنی دلتای آن صفر باشد.

b² - 4ac= 9 - 4(m -2).(m+2)= 0 --> m=⁺_- 2.5

با اشتراک دو شرط بالا فقط مقدار m=2.5 قابل قبول است

نقطه بحرانی

نقطه بحرانی:

نقاط بحرانی تابع f(x)= x^4/3 - x^2/3 در فاصله بسته 1- تا 1 کدامند؟

نکته : نقاطی که در آن مشتق تابع صفر شود ویا در آن نقاط مشتق وجود نداشته باشد و یا در آن نقاط مشتق بی نهایت شود نقاط بحرانی هستند.در ضمن نقاط دو سر بازه نیز نقاط بحرانی است.

بنابراین ابتدا مشتق تابع را می یابیم :

(f '(x)= (4/3)x^1/3 - (2/3)x^-1/3= (2/3)(2root³x - 1/root³x

و یا
f '(x)=2(2root³x² -1)/3root³x

توجه : منظور از root³x² ریشه سوم x² است.

دیده می شود که اولا" مشتق در x= 0 بی نهایت می شود و ثانیا" با صفر قرار دادن (f '(x داریم :

f '(x)= 0 --> 2root³x² =1 --> x²=1/8 --> x=⁺_- root2/4

بنابراین نقاط 0 و root2/4 و root2/4 - سه نقطه بحرانی تابع هستند.

قضیه مقدارمیانگین در مشتق:

قضیه مقدارمیانگین در مشتق:

تابع f با ضابطه f(x) = x²+x+1 در بازه بسته 1 تا a در نقطه c = 2 در قضیه مقدار میانگین برای مشتق صدق می کند. عدد a مربوط به این قضیه چیست؟

نکته : طبق قضیه مقدار میانگین در مشتق شیب خط مماس در c برابر شیب خط AB است.(بین x=1 و x= a )

ابتدا مقادیر تابع در این دو نقطه را می یابیم

f(1) = 3 , f(a) = a²+a+1

و شیب خط واصل بین این دو نقطه برابر است با

(m = (a²+a+1 - 3)/(a -1) = (a²+a - 2)/(a -1

سپس با مشتق گیری شیب خط مماس در نقطه c = 2 را می یابیم

f'(x) = 2x+1 --> f'(2) = 5

و در نتیجه
c (a²+a -2)/(a -1) = 5 --> a² - 4a+3 = 0

و یا
c (a - 3)(a -1) = 0 --> a =1 , a = 3

و طبیعی است که مقدار a = 3 قابل قبول است.

دو منحنی مماس:

دو منحنی مماس:

نمودارهای دو تابع با ضابطه های y = ax²+bx - 9 و y = x³/3 - 4x در نقطه ای به طول 3 مماس مشترک دارند. مقادیر a و b را بیابید.

نکته : دو منحنی مماس اولا" دارای نقطه تماس مشترک و ثانیا" دارای مماسهای برابر هستند.

بنابراین ابتدا در x = 3 دو مقدار تابع با هم برابرند

y₂ = y₁ --> x³/3 - 4x = ax²+bx - 9

و در نتیجه
9a+3b - 9 = 9 - 12 --> 3a+b = 2

و مساوی بودن مشتقها در همین نقطه

y₁' = y₂' --> 2ax+b = x² - 4

و در نتیجه
6a+b = 9 - 4 --> 6a+b = 5

و با حل دستگاه دو معادله دو مجهولی داریم

a = 1 , b = -1

خط قائم بر منحنی

خط قائم بر منحنی:

تعداد قائمهایی که از نقطه A(3,0)c بر منحنی تابع y² = 4x می توان رسم کرد چند تاست؟

نقطه A خارج منحنی است.

اگر عرض نقطه برخورد قائم را a فرض کنیم طول آن a²/4 خواهد بود.

و شیب خط قائم برابر است با

m' = (y₂ - y₁)/(x₂ - x₁) = (a - 0)/(a2/4 - 3)c

و یا
m' = 4a/(a² -12)c

از طرف دیگر با گرفتن مشتق از تابع نیز می توان این شیب را حساب کرد

2yy' = 4 --> y' = 2/y --> m = 2/a --> m' = - a/2

و با برابر قرار دادن این دو شیب داریم

4a/(a² -12) = - a/2 --> a³ - 4a = 0

و یا
a(a² - 4) = 0 --> a = 0 ; a = 2 ; a = - 2

بنابراین سه قائم می توان رسم کرد.

معادله سیاله

معادله سیاله یا معادلهٔ دیوفانتی در ریاضیات معادله‌ای‌ چند جمله‌ای با متغیرهای صحیح است که در آن بیش از یک متغیر (مجهول) داشته ‌باشیم. دستگاه معادلات دیوفانتی دستگاهی از معادلات چند مجهولی است که در آن تعداد مجهول‌ها از تعداد معادله‌ها بیشتر باشد.

مثلاً معادله‌ی x + y = 2 را می توان به صورت y = 2 − x نوشت. به ازای هر x یک مقدار برای y به دست می‌آید. این جوابها را می توان با زوج (x,2 − x) نشان داد. گر چه همین معادله، در مجموعه اعداد صحیح باز جوابهای بیشمار دارد، اما این بار در زوج (x,2 − x) باید به جای x اعداد صحیح قرار دهیم (از این نظر نسبت به حالت اوّل جوابها محدودتر هستند) و سرانجام اگر همین معادله را در اعداد طبیعی حل کنیم، معادله جواب کاملاً محدود و مشخصی پیدا می کند که در اینجا تنها جواب معادله ی x + y = 2 در اعداد طبیعی (1و1) است.

در اینجا حل معادله های دیوفانتی در مجموعه‌ی اعداد صحیح مورد نظر ماست و از این رو اگر در حالت کلی داشته باشیم ax + by = c که در آن a و b و c اعداد صحیح و a و b نسبت به هم اوّل هستند، آنگاه ریشه های این معادله در مجموعه اعداد صحیح به صورت زیر نوشته می شود.

                             y0 = y + ak و x0 = x − xk

که در آن (x0,y0) هر ریشه دلخواه معادله و (k عضو Zاست).

مثلاً یکی از ریشه های معادله x + 2y = 5 عبارت است از (2و1) پس زوج (1 − 2k,2 + k) در ازای هر k که k عضو اعداد صحیح است، یک جواب از این معادله به دست می آید. ممکن است معادله دیوفانتی از درجات بالاتر باشد، در این صورت هم امکان دارد معادله جوابهای بیشمار یا متناهی داشته باشد.

مثال:معادله 3x + 4y = 25 را در مجموعه اعداد صحیح حل کنید.

حل:معادله را به صورت زیر می نویسیم:

                                     3x = 25 − 4y   
                              x = (25 − 4y) / 3 = 8 + (1 − 4y) / 3

چون x عدد صحیح است، بنابراین 8 + (1 − 4y) / 3 باید عدد صحیح باشد، دیده می شود که به ازای y=+1 داریم x=8-1=7 پس (7,1) یکی از ریشه های معادله است و ریشه های دیگر معادله از زوج (x0 − bk,y0 + bk) محاسبه می شود که در آن k عضو اعداد صحیح است . پس سایر جوابهای معادله عبارتند از (7 − 4k,1 + 3k) مثلاً بعضی از ریشه های آن عبارتند از:

                                           k=1 بنابراین (4و3)
                                           k=2 بنابراین (2-و11)

ترکیبیات

ترکیبیات شاخه‌ای از ریاضیات است که به بررسی دسته‌هایی (معمولاً متناهی) از اشیا می‌پردازد که در شرایط معینی صدق می‌کنند. ریشه آن در روش‌های مربوط به شمردن دسته‌بندی‌های مختلف از اشیا یا افراد بوده‌است. امروز مبحث شمارش همهٔ ترکیبیات را در بر نمی‌گیرد بلکه ترکیبیات یکی از شاخه‌های بسیار وسیع عالم ریاضی است و شمارش بخشی از آن است.

شمارش و شمردن حالات انجام یک کار از زمانهای دور مورد بررسی بوده‌است. گویا این کار بیش از همه در جنگها برای شمارش سربازان به کار می‌رفته‌است.

در این قسمت روشهایی را برای شمردن بدون شمارش دانه به دانه معرفی می‌کنیم. ابتدا از دو اصل پر کاربرد شروع می‌کنیم:

۱) اصل ضرب: اصل ضرب می‌گوید که «اگر ما شی داشته و هر یک را به شی قسمت کنیم آنگاه شی خواهیم داشت».این اصل بسیار بدیهی است.حال ما آن را به صورتی پر کاربرد تر بیان می‌کنیم: «اگر پیشامدی به پیشامد پشت سر هم تقسیم گردد و پیشامد اول به حالت و پیشامد دوم به حالت واقع شود آنگاه کل پیشامد به حالت واقع می‌شود.»

مثال: شخصی قصد سفر از شهر به شهر و سپس شهر را دارد. از شهر به شهر ، پنج جاده و از به چهار راه وجود دارد. اگر از به جادهٔ مستقل وجود نداشته باشد به چند طریق می‌توان از به رفت؟ جواب: واضح است که بنا بر اصل ضرب پاسخ برابر ۲۰ می‌باشد. این ساده‌ترین نوع سوال ترکیبیات است.

در اصل شمارش اگر کاری را بتوان به طریق و کار دیگری را بتوان به طریق انجام داد و اگر این دو کار را نتوان هم‌زمان انجام داد آنگاه این یا آن کار را می‌توان به طریق انجام داد.

صُمٌ بُکمٌ عُمیٌ ...

سلام؛آقای مظلومان؛

امروز، شیعیانت، مظلوم‌تر و محروم‌تر و مغموم‌تر از هر زمان دیگرند.

کمر خم کرده‌اند زیر بار ظلم حاکمانِ دنیا؛ ضعیف نگاه داشته‌ شده‌اند؛ زجر می‌کشند...

آقا جان؛

آنان که به ناحق، تکیه بر کرسی حکومت دنیا زده‌اند، کر و لال و کورند.

صُمٌّ بُکْمٌ عُمْیٌ فَهُمْ لاَ یَرْجِعُونَ (بقره، 18)

در شنیدن ناله‌های مظلومان، کَرَند.  در پاسخ به سوالات محرومان، لال‌اند.

در دیدن دل‌های شکسته و زخم جگرهای پاره‌پاره‌ی مغمومان، کورند.

آقا جان، آنان که خون شیعیانت را می‌مکند، داعیه‌ی اصلاح دارند...

وَ إِذَا قِیلَ لَهُمْ لاَ تُفْسِدُواْ فِی الأَرْضِ قَالُواْ إِنَّمَا نَحْنُ مُصْلِحُونَ (بقره، 11)

آقای نازنین ما،

منتظریم تا فرارسیدن عذاب الهی؛ منتظریم تا رهایی..

خَتَمَ اللّهُ عَلَى قُلُوبِهمْ وَ عَلَى سَمْعِهِمْ وَ عَلَى أَبْصَارِهِمْ غِشَاوَةٌ

وَ لَهُمْ عَذَابٌ عظِیمٌ(بقره، 7)

بیا، آقا جان؛

تو را به مظلومیت مادرت، قسم؛ بیا.

اللّهم عجّل لولیّک الفرج.

نظریه مجموعه ها

آموزش مجموعه ها- نظریه مجموعه ها

« مجموعه چیست ؟ » یا « به چه چیزی مجموعه گفته می شود ؟ »

این ها اولین سوالاتی هستند که درباره ی مجموعه ها مطرح می شوند. ساده ترین پاسخی که به این گونه سوالات داده می شود، این است : « مجموعه گردایه ای از اشیاء است. » مثلا ً مجموعه ی کتاب های یک قفسه یا مجموعه ی پرتقال های موجود در یک جعبه میوه و ...

اما اگر کمی کنجکاو باشیم، می توانیم این سوال را مطرح کنیم که:« گردایه چیست؟ » . « گردایه، انبوهی از چیزهاست. » و ...

اگر همچنان به کنجکاوی خود ادامه دهیم، در پاسخ به این قبیل سوالات، تعدادی از کلمات ِ هم معنی با مجموعه ردیف خواهد شد و پس از چند کلمه، به جایی می رسیم که مجبور خواهیم شد دوباره از کلمه ی مجموعه استفاده کنیم. به این ترتیب به تعریفی دوری برای مجموعه خواهیم رسید که از لحاظ منطقی بی ارزش خواهد بود. چاره چیست ؟

در چنین مواردی ، نیاز به مفاهیم اولیه ای است که آن ها را بدون تعریف می پذیریم، با این فرض که برداشت های افراد از این مفاهیم ، به قدر کافی به یکدیگر شبیه است و هیچ ابهامی در فهم آن ها وجود ندارد. گاهی نیز برای رفع ابهام و مشخص تر کردن منظور، تعریفی صوری برای این مفاهیم می آورند.

ما مجموعه را جزء مفاهیم اولیه می دانیم و تعریفی برای آن ارائه نمی دهیم. اما ریاضی دان نامی، کانتور، تعریف زیر را برای مجموعه ارائه کرده است :

کانتور می گوید : « مجموعه گردایه ای از اشیاء متمایز در شعور ماست که به این اشیای ِ مجزا، اعضای مجموعه می گوییم. »

تعریف گراف

تعاریف گراف

یک گراف شامل دو مجموعه است؛ مجموعه غیر تهی از گره ها یا رئوس (vertex) و مجموعه ای از یال ها (edge) که راس ها را به هم متصل می کنند.

مثال. می توان شهر های یک کشور را رئوس و جاده های بین آن ها را یال های یک گراف تصور کرد.

به هر راس یا هر یال گراف نامی اختصاص داده می شود.

یک گراف تهی (null graph) گرافی است که تنها شامل راس است و مجموعه یال های آن تهی است یعنی یالی ندارد.

جهت

یک گراف می تواند به دو شکل جهتدار(directed) یا غیرجهتدار (undirected) باشد.

یک گراف جهتدار گرافی است که جهت هر یال در آن تعیین شده است. در گراف جهتدار ترتیب رئوس در هر یال اهمیت دارد و یال ها با پیکان هائی از راس ابتدا به راس انتها رسم می شوند. در گراف غیرجهتدار می توان در هر دو جهت بین راس ها حرکت کرد و ترتیب راس های یال اهمیت ندارد.

نظریه گراف

تعریف

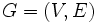فرض کنید V یک مجموعه ناتهی و E زیرمجموعه‌ای از باشد در این صورت زوج را یک گراف می نامند.V را مجموعه راس ها و E را مجموعه یال ها می گویند. اگر ترتیب قرار گرفتن راس ها در مجموعه E مهم باشد،گراف را گراف جهت‌دار می گویند و یال از راس 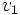به سمت راس 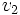را به صورت 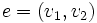نشان می‌دهند.در غیر این صورت گراف را بدون جهت می‌نامند و یال بین راس های 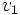و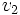 با نماد 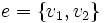نشان می‌دهند.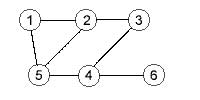

تعداد راس های یک گراف را مرتبه و تعداد یال های آن را اندازه گراف می نامیم.
در شکل روبرو گرافی را با شش راس و هفت یال مشاهده می کنیم انواع گراف‌ها

گراف‌ها دارای انواع متعددی هستند که به برخی از آنها اشاره می‌کنیم:

• گراف همبند
• گراف ناهمبند
• گراف اویلری
• گراف همیلتونی
• گراف درختی
• گراف مسطح
• گراف چندبخشی
• گراف k-مکعب
• گراف ستاره‌ای
• گراف اشتراکی
• گراف منظم
• گراف جهت‌دار

گراف‌ها و ساختار داده‌ها

هر گراف را می‌توان با یک ماتریس نمایش داد ، که به آن گویند. در این روش از آرایه هااستفاده می‌کنیم.این ماتریس به تعداد راس‌های گراف دارای سطر و ستون است.وعدد 1 نشان دهنده وجود یک یال بین دو راس و عدد 0 نشان دهنده عدم وجود ارتباط بین دو راس است.یعنی ماتریس ما شامل دو عدد صفر و یک است. با استفاده از این ماتریس می‌توان رئوسی را که با یک راس در ارتباط‌اند و نیز رئوسی را که با هیچ راس دیگری ارتباط ندارند رامشخص کرد.

گراف

در نظریه گراف، یک درخت گرافی است که هر دو راس آن بوسیله دقیقاً یک یال به هم متصل شده اند، یک جنگل گرافی است که دو راس آن با بیشتر از یک راس به هم متصل اند. یک جنگل در واقع از اتصال، مجموعه ای از درخت ها به وجود می آید.

تعریف ها:
یک درخت از شرایط زیر پیروی می کند.

در آن هیچ مدار یا حلقه ای موجود نیست.
درخت یک گراف همبند است.
با حذف یک یال از درخت، دیگر آن گراف یک درخت نخواهد بود.
هر دو راس در یک درحت بوسیله مسیر منحصر به فرد به هم متصل می شوند.

اگر یک جنگل با n راس باشد آن گاه از شرایط زیر پیروی می کند:

T یک درخت است.
T مداری ندارد و n-1 یال دارد.
T همبند است و n-1 یال دارد.
هر دو راس T با مسیر منحصر به فرد به هم متصل می شوند.
T مداری ندارد و با افزودن یگ یال جدید دقیقاً یک مدار بوجود می آید.

هندسه ها

در جدول زیر هر سه هندسه ها با یکدیگر مقایسه شده اند:

نوع هندسه	تعداد خطوط موازی	مجموع زوایای مثللث	نسبت محیط به قطر دایره
اقلیدسی	یک	180	عدد پی
هذلولوی	بینهایت	< 180	> عدد پی
بیضوی	صفر	> 180	< عدد پی

چهارضلعی خیام-ساکری

پرش به: ناوبری، جستجو

چهارضلعی خیام-ساکری (Saccheri quadrilateral) را نخستین بار عمر خیام مورد بحث قرار داد اما در غرب با کارهای ساکری معرفی شد. خیام این چهارضلعی را بیش از هفت سده قبل از ساکری در کتاب «شرح ما اشکل» مطرح کرده است ساکری ریاضیدان ایتالیایی و نویسنده کتاب «اقلیدوس به دور از همه نارسایی ها» در سال ۱۷۷۳ بود.

هندسه‌ای که اقلیدس بنا نهاد بر پنج اصل موضوع (بنداشت) بنا شده است. ریاضیدانان حتا قبل از تدوین این اصول توسط اقلیدس بر سر چهار اصل نخست توافق داشتند اما اصل پنجم از همان دوران تا هنگامی که در اواخر قرن هفدهم با ظهور هندسه‌های نااقلیدسی برای همیشه حل شود مورد مناقشه بود. ریاضی‌دانان تلاش می‌کردند اصل پنجم را که به نظرشان پیچیده می‌آمد با توجه به چهار اصل نخست مانند سایر قضایا اثبات کنند. جیرولامو ساکری تلاش کرد با طرح چهار ضلعی‌یی از طریق برهان خلف این اصل را از چهار اصل قبلی نتیجه بگیرد. او برای اثبات اصل پنجم از روی چهار اصل اول، و بیست و هشت قضیهٔ منتج از آن‌ها، (هندسهٔ نتاری) چهار ضلعی را در نظر گرفت که زوایای A و B قائمه و اضلاع AD و BC برابرند. ساکری با رسم قطر AC و BD و با استفاده از قضایای هم‌نهشتی ساده (از بین بیست و هشت قضیهٔ اول) به آسانی نشان داد که زاویه C و D برابر هستند. بنا بر این سه امکان پیش می‌آید زوایای C و D حاده باشند، قائمه باشند یا منفرجه باشند.

امام زمان

میدان

میدان

 

تعریف: نیم گروهی که عضو خنثی و هر عضو ان وارون پذیر باشد را گروه گوییم.اگر عمل تعریف شده روی مجموعه خاص جا به جایی باشد گروه را جا به جایی یا ابلی می گوییم.

تعریف: فرض کنید R یک مجموعه نا تهی باشد و + و . به عنوان دو عمل که اولی عمل جمع و دومی عمل ضرب تعریف شوند. به ساختمان ریاضی ( . , + , R ) یک حلقه گوییم هرگاه شرایط زیر برقرار باشند :

۱) (+,R ) یک گروه جابه جایی باشد.

۲) ( .,R ) یک نیم گروه باشد.

۳) R با دو عمل تعریف شده خاصیت پخشی داشته باشد. یعنی اگر a,b,c سه عضو دلخواه متعلق به R باشند ان وقت :

a . (b+c) = a.b + a.c و b+c).a = b.a + c.a)

تعریف: حلقه R را بدیهی گوییم هرگاه ضرب هر دو عنصر دلخواه ان صفر باشد(عضو همانی)

تعریف: حلقه R را جا به جایی گوییم هر گاه نیم گروه ضربی جا به جایی باشد.

تعریف: حلقه R را یکه دار گوییم هر گاه نیم گروه ضربی عضو خنثی یا همانی داشته باشد.

تعریف: حلقه R را میدان گوییم اگر عضو خنثی جمعی را از نیم گروه ضربی خارج کنیم گروه جا به جایی تولید شود.

تعریف: حلقه R را حوزه صحیح گوییم اگرx , y متعلق به R باشند و x.y = 0 ایجاب کند x = 0 یا y = 0 .

تمرین: ایا x.y =0 لزوما ایجاب می کند x = 0 یا y = 0