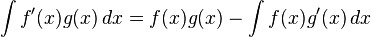علم ریاضی

این وبلاگ جهت استفاده علاقمندان به ریاضی ایجاد شده است.

علم ریاضی

این وبلاگ جهت استفاده علاقمندان به ریاضی ایجاد شده است.

فرمول های انتگرال

$\int {f'(x)\over f(x)}\,dx= \ln{\left|f(x)\right|} + C$ $\int {f'(x) f(x)}\,dx= {1 \over 2} [ f(x) ]^2 + C$ $\int [f(x)]^n f'(x)\,dx = {[f(x)]^{n+1} \over n+1} + C \qquad\mbox{(for } n\neq -1\mbox{)}\,\!$

Rational functions

$\int \,{\rm d}x = x + C$

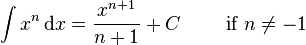
$\int x^n\,{\rm d}x = \frac{x^{n+1}}{n+1} + C\qquad\mbox{ if }n \ne -1$

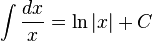
$\int {dx \over x} = \ln{\left|x\right|} + C$

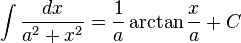
$\int {dx \over {a^2+x^2}} = {1 \over a}\arctan {x \over a} + C$

Irrational functions

$\int {dx \over \sqrt{a^2-x^2}} = \sin^{-1} {x \over a} + C$

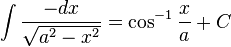
$\int {-dx \over \sqrt{a^2-x^2}} = \cos^{-1} {x \over a} + C$

$\int {dx \over x \sqrt{x^2-a^2}} = {1 \over a} \sec^{-1} {|x| \over a} + C$

Logarithms

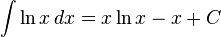
$\int \ln {x}\,dx = x \ln {x} - x + C$

$\int \log_b {x}\,dx = x\log_b {x} - x\log_b {e} + C$

Exponential functions

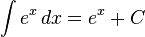
$\int e^x\,dx = e^x + C$

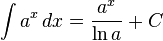
$\int a^x\,dx = \frac{a^x}{\ln{a}} + C$

Trigonometric functions

$\int \sin{x}\, dx = -\cos{x} + C$

$\int \cos{x}\, dx = \sin{x} + C$

$\int \tan{x} \, dx = -\ln{\left| \cos {x} \right|} + C$

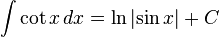
$\int \cot{x} \, dx = \ln{\left| \sin{x} \right|} + C$

$\int \sec{x} \, dx = \ln{\left| \sec{x} + \tan{x}\right|} + C$

$\int \csc{x} \, dx = \ln{\left| \csc{x} - \cot{x}\right|} + C$

$\int \sec^2 x \, dx = \tan x + C$

$\int \csc^2 x \, dx = -\cot x + C$

$\int \sec{x} \, \tan{x} \, dx = \sec{x} + C$

$\int \csc{x} \, \cot{x} \, dx = - \csc{x} + C$

$\int \sin^2 x \, dx = \frac{1}{2}(x - \sin x \cos x) + C$

$\int \cos^2 x \, dx = \frac{1}{2}(x + \sin x \cos x) + C$

$\int \sec^3 x \, dx = \frac{1}{2}\sec x \tan x + \frac{1}{2}\ln|\sec x + \tan x| + C$

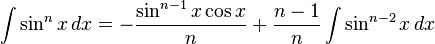
$\int \sin^n x \, dx = - \frac{\sin^{n-1} {x} \cos {x}}{n} + \frac{n-1}{n} \int \sin^{n-2}{x} \, dx$

$\int \cos^n x \, dx = \frac{\cos^{n-1} {x} \sin {x}}{n} + \frac{n-1}{n} \int \cos^{n-2}{x} \, dx$

$\int \arctan{x} \, dx = x \, \arctan{x} - \frac{1}{2} \ln{\left| 1 + x^2\right|} + C$

Hyperbolic functions

$\int \sinh x \, dx = \cosh x + C$

$\int \cosh x \, dx = \sinh x + C$

$\int \tanh x \, dx = \ln| \cosh x | + C$

$\int \mbox{csch}\,x \, dx = \ln\left| \tanh {x \over2}\right| + C$

$\int \mbox{sech}\,x \, dx = \arctan(\sinh x) + C$

$\int \coth x \, dx = \ln| \sinh x | + C$

$\int \mbox{sech}^2 x\, dx = \tanh x + C$

Inverse hyperbolic functions

$\int \operatorname{arcsinh} x \, dx = x \operatorname{arcsinh} x - \sqrt{x^2+1} + C$

$\int \operatorname{arccosh} x \, dx = x \operatorname{arccosh} x - \sqrt{x^2-1} + C$

$\int \operatorname{arctanh} x \, dx = x \operatorname{arctanh} x + \frac{1}{2}\log{(1-x^2)} + C$

$\int \operatorname{arccsch}\,x \, dx = x \operatorname{arccsch} x+ \log{\left[x\left(\sqrt{1+\frac{1}{x^2}} + 1\right)\right]} + C$

$\int \operatorname{arcsech}\,x \, dx = x \operatorname{arcsech} x- \arctan{\left(\frac{x}{x-1}\sqrt{\frac{1-x}{1+x}}\right)} + C$

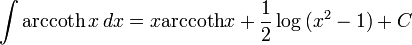
$\int \operatorname{arccoth}\,x \, dx = x \operatorname{arccoth} x+ \frac{1}{2}\log{(x^2-1)} + C$

Definite integrals lacking closed-form antiderivatives

$\int_0^\infty{\sqrt{x}\,e^{-x}\,dx} = \frac{1}{2}\sqrt \pi$

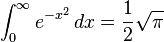
$\int_0^\infty{e^{-x^2}\,dx} = \frac{1}{2}\sqrt \pi$

$\int_0^\infty{\frac{x}{e^x-1}\,dx} = \frac{\pi^2}{6}$

$\int_0^\infty{\frac{x^3}{e^x-1}\,dx} = \frac{\pi^4}{15}$

$\int_0^\infty\frac{\sin(x)}{x}\,dx=\frac{\pi}{2}$

$\int_0^\frac{\pi}{2}\sin^n{x}\,dx=\int_0^\frac{\pi}{2}\cos^n{x}\,dx=\frac{1 \cdot 3 \cdot 5 \cdot \cdots \cdot (n-1)}{2 \cdot 4 \cdot 6 \cdot \cdots \cdot n}\frac{\pi}{2}$ (if n is an even integer and $\scriptstyle{n \ge 2}$ )

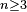$\int_0^\frac{\pi}{2}\sin^n{x}\,dx=\int_0^\frac{\pi}{2}\cos^n{x}\,dx=\frac{2 \cdot 4 \cdot 6 \cdot \cdots \cdot (n-1)}{3 \cdot 5 \cdot 7 \cdot \cdots \cdot n}$ (if $\scriptstyle{n}$ is an odd integer and $\scriptstyle{n \ge 3}$ )

$\int_0^\infty\frac{\sin^2{x}}{x^2}\,dx=\frac{\pi}{2}$

$\int_0^\infty x^{z-1}\,e^{-x}\,dx = \Gamma(z)$

$\int_{-\infty}^\infty e^{-(ax^2+bx+c)}\,dx=\sqrt{\frac{\pi}{a}}\exp\left[\frac{b^2-4ac}{4a}\right]$

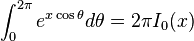
$\int_{0}^{2 \pi} e^{x \cos \theta} d \theta = 2 \pi I_{0}(x)$

$\int_{0}^{2 \pi} e^{x \cos \theta + y \sin \theta} d \theta = 2 \pi I_{0} \left(\sqrt{x^2 + y^2}\right)$

$\int_{-\infty}^{\infty}{(1 + x^2/\nu)^{-(\nu + 1)/2}dx} = \frac { \sqrt{\nu \pi} \ \Gamma(\nu/2)} {\Gamma((\nu + 1)/2))}\,$ ( $\nu > 0\,$ ,

$\int_a^b{f(x)\,dx} = (b - a) \sum\limits_{n = 1}^\infty {\sum\limits_{m = 1}^{2^n - 1} {\left( { - 1} \right)^{m + 1} } } 2^{ - n} f(a + m\left( {b - a} \right)2^{-n} )$

$\begin{align} \int_0^1 x^{-x}\,dx &= \sum_{n=1}^\infty n^{-n} &&(= 1.291285997\dots)\\ \int_0^1 x^x \,dx &= \sum_{n=1}^\infty -(-1)^nn^{-n} &&(= 0.783430510712\dots) \end{align}$